Question

【題目】（實驗操作）如圖①，在中，，現將邊沿的平分線翻折，點落在邊的點處；再將線段沿翻折到線段，連接.

（探究發現）若點，，三點共線，則的大小是______，的大小是________，此時三條線段，，之間的數量關系是________.

（應用拓展）如圖②，將圖①中滿足（實驗操作）與（探究發現）的的邊延長至，使得，連接，直接寫出的度數.

Answer 1

【答案】【探究發現】60°，100°，BC=BD+AD；【應用拓展】∠BCE=10°.

【解析】

探究發現：根據折疊性質可得∠ADB=∠BDA1，∠A1DC=∠CDA2，由B、D、A2在一條直線上可得∠CDA2=∠ADB，可得∠ADB=∠BDA1=∠A1DC=∠CDA2，根據平角定義可求出∠CDA2的度數即可得∠ADB的度數；根據外角性質及等腰三角形的性質即可求出∠BAC的度數；根據折疊性質可得AD=A1D=A2D，可得BD+AD=BA2，根據折疊性質可求出∠A2CB=∠BA2C，根據等腰三角形的性質即可得BC=BD+AD；應用拓展：以BC為邊，在△ABC外作等邊△BCD，連接AD，利用SSS可證明△ABD≌△ACD，可得∠ADB=∠ADC=∠BDC=30°，根據等腰三角形的性質可求出∠ABC=∠ACB=40°，可得∠ACD=∠BAC=100°，由AE=BC可得AE=CD，利用SAS可證明△AEC≌△CDA，可得∠AEC=∠ADC=30°，利用外角性質求出∠BCE的度數即可.

探究發現：

∵邊沿的平分線翻折，點落在邊的點處，

∴∠ADB=∠A1DB，

∵線段沿翻折到線段，

∴∠A1DC=∠A2DC，

∵B、D、A2三點共線，

∴∠ADB=∠A2DC，

∴∠A1DB=∠A1DC=∠A2DC，

∴∠A1DB=×180°=60°，

∴∠ADB=60°，

∵AB=AC，

∴∠ABC=（180°-∠BAC），

∵BD是∠ABC的角平分線，

∴∠ABD=∠ABC=（180°-∠BAC），

∴∠BDC=∠ABD+∠BAC=（180°-∠BAC）+∠BAC=120°，

解得：∠BAC=100°，

根據折疊性質得：∠BA1D=∠BAC=100°，AD=A1D=A2D，∠BCA=∠ACA2=40°，

∴BD+AD=BD+A2D=BA2，∠A2=∠DA2C=180°-∠BA1D=80°，∠BCA2=2∠BCA=80°，

∴∠A2=∠BCA2，

∴BC=BA2，

∴BC=BD+AD.

故答案為：60°，100°，BC=BD+AD

應用拓展：

以BC為邊，在△ABC外作等邊△BCD，連接AD，

∴BC=BD=CD，

∵AB=AC，BD=CD，AD=AD，

∴△ABD≌△ACD，

∴∠ADB=∠ADC=∠BDC=30°，

∵∠ACB=∠ABC=40°，△BCD是等邊三角形，

∴∠DCA=∠BAC=100°，

∵AE=BC，

∴AE=CD，

在△AEC和△CDA中，，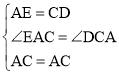

∴△AEC≌△CDA，

∴∠AEC=∠ADC=30°，

∴∠BCE=∠ABC-∠AEC=40°-30°=10°.