
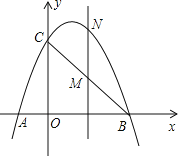
【題目】如圖,已知拋物線經過點A(-1,0)、B(3,0)、C(0,3)三點。
(1)求拋物線的解析式。
(2)點M是線段BC上的點(不與B,C重合),過M作MN∥y軸交拋物線于N若點M的橫坐標為m,請用m的代數式表示MN的長。
(3)在(2)的條件下,連接NB、NC,是否存在m,使△BNC的面積最大?若存在,求m的值;若不存在,說明理由。
【答案】(1)y=﹣x2+2x+3.(2) ﹣m2+3m(0<m<3).(3) 當m=![]() 時,△BNC的面積最大,最大值為
時,△BNC的面積最大,最大值為![]() .
.
【解析】試題分析:(1)利用待定系數法求二次函數的解析式;
(2)先求直線BC的解析式,表示出M、N兩點的坐標,利用縱坐標的差計算MN的長即可;
(3)根據面積公式得:S△BNC=S△CMN+S△MNB=![]() |MN||OB|,OB的長是定值為3,所以MN的最大值即為面積的最大值,求MN所表示的二次函數的最值即可.
|MN||OB|,OB的長是定值為3,所以MN的最大值即為面積的最大值,求MN所表示的二次函數的最值即可.
解:(1) ∵拋物線經過點A(1,0),B(3,0),C(0,3)三點,
∴設拋物線的解析式為:y=a(x+1)(x3),
把C(0,3)代入得:3=a(0+1)(03),
a=1,
∴拋物線的解析式:y=-x2+2x+3
(2) 設直線BC的解析式為:y=kx+b,
把B(3,0),C(0,3)代入得: ![]() ,
,
解得:
![]() ,
,
∴直線BC的解析式為y=-x+3,
∴M(m,-m+3),
又∵MN⊥x軸,
∴N(m,-m2+2m+3),
∴MN=(-m2+2m+3)-(-m+3)=-m2+3m(0<m<3)
(3)S△BNC=S△CMN+S△MNB=![]() |MN|·|OB|,
|MN|·|OB|,
∴當|MN|最大時,△BNC的面積最大,
MN=-m2+3m=-(m-![]() )2+
)2+![]() ,
,
所以當m=![]() 時,△BNC的面積最大為
時,△BNC的面積最大為![]() ×
×![]() ×3=
×3=![]()


科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+2ax+1與x軸僅有一個公共點A,經過點A的直線交該拋物線于點B,交y軸于點C,且點C是線段AB的中點.

(1)求這條拋物線對應的函數解析式;
(2)求直線AB對應的函數解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
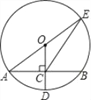
【題目】如圖,⊙O的半徑OD⊥弦AB于點C,連結AO并延長交⊙O于點E,連結EC.若AB=8,CD=2,則EC的長為( )
A. 2![]() B. 8 C. 2
B. 8 C. 2![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,正方形ABCD的邊長等于2,它繞頂點B按順時針方向旋轉得到正方形A′BC′D′.在這個旋轉過程中:
(1)旋轉中心是什么?
(2)若旋轉角為45°,邊CD與A′D′交于F,求DF的長度.

![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com