
分析 (1)由已知等式知,連續奇數乘積的倒數等于各自倒數差的一半,據此可得;
(2)根據以上規律可得原式=$\frac{1}{2}$×(1-$\frac{1}{3}$)+$\frac{1}{2}$×($\frac{1}{3}$-$\frac{1}{5}$)+$\frac{1}{2}$×($\frac{1}{7}$-$\frac{1}{9}$)+…+$\frac{1}{2}$($\frac{1}{199}$-$\frac{1}{201}$)=$\frac{1}{2}$×(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{199}$-$\frac{1}{201}$),即可得出答案.
解答 解:(1)由已知等式知,連續奇數乘積的倒數等于各自倒數差的一半,
∴第n個等式為$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$);
(2)原式=$\frac{1}{2}$×(1-$\frac{1}{3}$)+$\frac{1}{2}$×($\frac{1}{3}$-$\frac{1}{5}$)+$\frac{1}{2}$×($\frac{1}{7}$-$\frac{1}{9}$)+…+$\frac{1}{2}$($\frac{1}{199}$-$\frac{1}{201}$)
=$\frac{1}{2}$×(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{199}$-$\frac{1}{201}$)
=$\frac{1}{2}$×(1-$\frac{1}{201}$)
=$\frac{1}{2}$×$\frac{200}{201}$
=$\frac{100}{201}$.
點評 本題主要考查數字的變化規律,根據題意得出連續奇數乘積的倒數等于各自倒數差的一半且掌握裂項求和是解題的關鍵.


科目:初中數學 來源: 題型:解答題
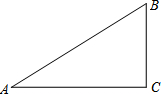 已知:如圖,在△ABC中,∠A=30°,∠B=60°.
已知:如圖,在△ABC中,∠A=30°,∠B=60°.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com