與直線
在第二象限的交點，AB⊥
軸于B，且
。求這兩個函數的解析式。
沖刺100分單元優化練考卷系列答案科目：初中數學 來源： 題型：
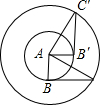如圖，Rt△AB′C′是Rt△ABC以點A為中心逆時針旋轉90°而得到的，其中AB=1，BC=2，則旋轉過程中弧CC′的長為（ ）A、
| ||||
B、
| ||||
| C、5π | ||||
D、
|
查看答案和解析>>
科目：初中數學 來源：非常講解·教材全解全析 數學 七年級下 （配北師大課標） 北師大課標 題型：022
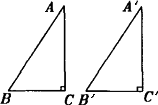
如圖，在△ABC和△
中，∠C＝∠
＝90°．
①∵AB＝
，BC＝
(已知)，
∴Rt△ABC≌△Rt△( )．
②∵AB＝
，AC＝
(已知)，
∴Rt△ABC≌Rt△( )．
③∵AC＝
，BC＝
(已知)，
∴Rt△ABC≌Rt△( )．
④∵∠A＝∠
，AB＝
(已知)，
∴Rt△ABC≌Rt△( )．
⑤∵∠B＝∠
，BC＝
(已知)，
∴Rt△ABC≌△Rt△( )．
查看答案和解析>>
科目：初中數學 來源：數學教研室 題型：044
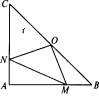
①寫出點O到△ABC的三個頂點A、B、C的距離的關系(不要求證明)；
②如果點M、N分別在線段AB、AC上移動，在移動中保持AN=BM請判斷△OMN的形狀，并證明你的結論．
查看答案和解析>>
科目：初中數學 來源：三點一測叢書 九年級數學 上 （江蘇版課標本） 江蘇版課標本 題型：059
如圖，已知：如圖(1)，AB是⊙O的直徑，P是AB上的一點(與A、B不重合)．QP⊥AB，垂足為P，直線QA交⊙O于C點，過C點作⊙O的切線交直線QP于點D，則△CDQ是等腰三角形．對上述命題證明如下：
證明：連結OC．
∵OA＝OC，∴∠A＝∠1．
∵CD切⊙O于C點，
∴∠OCD＝90°，
∴∠1＋∠2＝90°，
∴∠A＋∠2＝90°．
在Rt△QPA中，∠QPA＝90°，
∴∠A＋∠Q＝90°，
∴∠2＝∠Q．∴DQ＝DC．
即△CDQ是等腰三角形．
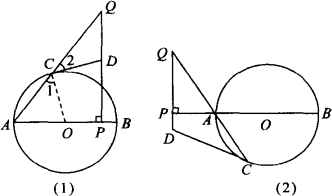
問題：對上述命題，當點P在BA的延長線上時，其他條件不變，如圖(2)所示，結論“△CDQ是等腰三角形”還成立嗎？若成立，請給予證明；若不成立，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
，可得
，
，
，所以
，
。
