
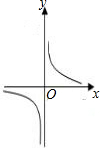
 如圖,這是函數( )的大致圖象.
如圖,這是函數( )的大致圖象.| A、y=-5x | ||
| B、y=2x+8 | ||
C、y=
| ||
D、y=-
|
科目:初中數學 來源:初中數學 三點一測叢書 八年級數學 下 (江蘇版課標本) 江蘇版 題型:013
反比例函數y=![]() (k≠0)任取一點M(a,b),過M作MA⊥x軸,MB⊥y軸,所得矩形OAMB的面積為S=MA·MB=|b|·|a|=|ab|.又因為b=
(k≠0)任取一點M(a,b),過M作MA⊥x軸,MB⊥y軸,所得矩形OAMB的面積為S=MA·MB=|b|·|a|=|ab|.又因為b=![]() ,故ab=k,所以S=|k|(如圖(1)).
,故ab=k,所以S=|k|(如圖(1)).
這就是說,過雙曲線上任意一點作x軸、y軸的垂線,所得的矩形面積為|k|.這就是k的幾何意義,會給解題帶來方便.現舉例如下:
例1:如(2)圖,已知點P1(x1,y1)和P2(x2,y2)都在反比例函數y=![]() (k<0)的圖像上,試比較矩形P1AOB與矩形P2COD的面積大小.
(k<0)的圖像上,試比較矩形P1AOB與矩形P2COD的面積大小.
解答:![]() =|k|
=|k|
![]() =|k|
=|k|
故![]() =
=![]()

例2:如圖(3),在y=![]() (x>0)的圖像上有三點A、B、C,經過三點分別向x軸引垂線,交x軸于A1、B1、C1三點,連結OA、OB、OC,記△OAA1、△OBB1、△OCC1的面積分別為S1、S2、S3,則有( )
(x>0)的圖像上有三點A、B、C,經過三點分別向x軸引垂線,交x軸于A1、B1、C1三點,連結OA、OB、OC,記△OAA1、△OBB1、△OCC1的面積分別為S1、S2、S3,則有( )

A.S1=S2=S3
B.S1<S2<S3
C.S3<S1<S2
D.S1>S2>S3
解答:∵![]() =
=![]() |k|=
|k|=![]() ,
,
![]() =
=![]() |k|=
|k|=![]()
![]() =
=![]() |k|=
|k|=![]()
S1=S2=S3,故選A.
例3:一個反比例函數在第三象限的圖像如圖(4)所示,若A是圖像任意一點,AM⊥x軸,垂足為M,O是原點,如果△AOM的面積是3,那么這個反比例函數的解析式是________.

解答:∵S△AOM=![]() |k|
|k|
又S△AOM=3,
∴![]() |k|=3,|k|=6
|k|=3,|k|=6
∴k=±6
又∵曲線在第三象限
∴k>0∴k=6
∴所以反比例函數的解析式為y=![]() .
.
根據是述意義,請你解答下題:
如圖(5),過反比例函數y=![]() (x>0)的圖像上任意兩點A、B分別作軸和垂線,垂足分別為C、D,連結OA、OB,設AC與OB的交點為E,△AOE與梯形ECDB的面積分別為S1、S2,比較它們的大小,可得
(x>0)的圖像上任意兩點A、B分別作軸和垂線,垂足分別為C、D,連結OA、OB,設AC與OB的交點為E,△AOE與梯形ECDB的面積分別為S1、S2,比較它們的大小,可得

A.S1>S2
B.S1=S2
C.S1<S2
D.大小關系不能確定
查看答案和解析>>
科目:初中數學 來源: 題型:044
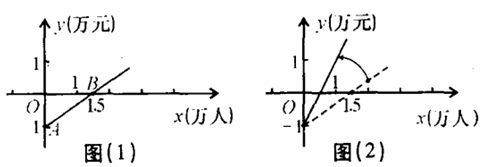
如圖( l )是某公共汽車線路收支差額y(票價總收人減去運營成本)與乘客量 x 的函數圖象.目前這條線路虧損,為了扭虧,有關部門舉行提高票價的聽證會.
乘客代表認為:公交公司應節約能源,改善管理,降低運營成本,以此舉實現扭虧.
公交公司認為:運營成本難以下降,公司己盡力,提高票價才能扭虧.
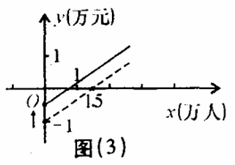
根據這兩種意見,可以把圖( l )分別改畫成圖( 2 )和圖( 3 ) ,
( l )說明圖( 1 )中點 A 和點 B 的實際意義:
( 2 )你認為圖( 2 )和圖( 3 )兩個圖象中,反映乘客意見的是 ,反映公交公司意見的是 .
( 3 )如果公交公司采用適當提高票價又減少成本的辦法實現扭虧為贏,請你在圖(4)中畫出符合這種辦法的 y 與 x 的大致函數關系圖象。

查看答案和解析>>
科目:初中數學 來源:2013屆四川雙流縣環佳中學八年級下學期期中考試數學卷(解析版) 題型:選擇題
函數y1 = x + 1與y2 = ax + b(a≠0)的圖象如圖所示,這兩個函數圖象的交點在y軸上,那么使y1,y2的值都大于零的x的取值范圍是( )
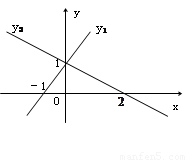
A、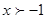 B、
B、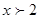
C、 D、
D、
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com