
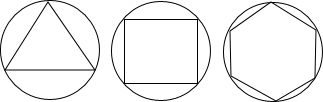
 法是否合理?若不合理,請給出正n邊形“接近度”的一個合理定義.
法是否合理?若不合理,請給出正n邊形“接近度”的一個合理定義. =162°,
=162°,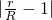 、
、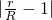 越小,正n邊形越接近于圓;
越小,正n邊形越接近于圓;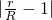 越大,正n邊形與圓的形狀差異越大;當
越大,正n邊形與圓的形狀差異越大;當 =1時,正n邊形就變成了圓.
=1時,正n邊形就變成了圓.

 華東師大版一課一練系列答案
華東師大版一課一練系列答案科目:初中數學 來源: 題型:
 20、如圖:將邊長為1的正三角形OAP,沿x軸正方向連續翻轉若干次,點A依次落在點A1,A2,A3,A4,…,A2008的位置上,則點A2008的橫坐標x2008=
20、如圖:將邊長為1的正三角形OAP,沿x軸正方向連續翻轉若干次,點A依次落在點A1,A2,A3,A4,…,A2008的位置上,則點A2008的橫坐標x2008=查看答案和解析>>
科目:初中數學 來源: 題型:
 18、如圖,將邊長為1的正三角形OAP沿x軸正方向連續翻轉2009次,點P依次落在點P1,P2,P3,…,P2009的位置,則點P2009的橫坐標為
18、如圖,將邊長為1的正三角形OAP沿x軸正方向連續翻轉2009次,點P依次落在點P1,P2,P3,…,P2009的位置,則點P2009的橫坐標為查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,用兩段等長的鐵絲恰好可以分別圍成一個正三角形和一個正方形,其中正三角形的邊長為(x2+15)cm,正方邊形的邊長為(x2+x)cm(其中x>0).則這兩段鐵絲的總長是
如圖,用兩段等長的鐵絲恰好可以分別圍成一個正三角形和一個正方形,其中正三角形的邊長為(x2+15)cm,正方邊形的邊長為(x2+x)cm(其中x>0).則這兩段鐵絲的總長是查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com