
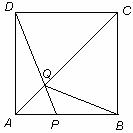
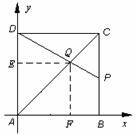
如圖,在邊長為4的正方形![]() 中,點
中,點![]() 在
在![]() 上從
上從![]() 向
向![]() 運動,連接
運動,連接![]() 交
交![]() 于點
于點![]() .
.
(1)試證明:無論點![]() 運動到
運動到![]() 上何處時,都有△
上何處時,都有△![]() ≌△
≌△![]() ;
;
(2)當點![]() 在
在![]() 上運動到什么位置時,△
上運動到什么位置時,△![]() 的面積是正方形
的面積是正方形![]() 面積的
面積的![]() ;
;
(3)若點![]() 從點
從點![]() 運動到點
運動到點![]() ,再繼續在
,再繼續在![]() 上運動到點
上運動到點![]() ,在整個運動過程中,當點
,在整個運動過程中,當點![]() 運動到什么位置時,△
運動到什么位置時,△![]() 恰為等腰三角形.
恰為等腰三角形.
(1)證明:在正方形![]() 中,無論點
中,無論點![]() 運動到
運動到![]() 上何處時,都有
上何處時,都有
![]() =
=![]() ∠
∠![]() =∠
=∠![]()
![]() =
=![]()
∴△![]() ≌△
≌△![]()
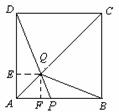
(2)解法一:△![]() 的面積恰好是正方形ABCD面積的
的面積恰好是正方形ABCD面積的![]() 時,
時,
過點Q作![]()
![]() ⊥
⊥![]() 于
于![]() ,
,![]() ⊥
⊥![]() 于
于![]() ,則
,則![]() =
= ![]()
![]()
![]() =
=![]() =
=![]()
∴![]() =
=![]()
由△![]() ∽△
∽△![]() 得
得 ![]() 解得
解得![]()
∴![]() 時,△
時,△![]() 的面積是正方形
的面積是正方形![]() 面積的
面積的![]()
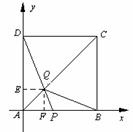
解法二:以![]() 為原點建立如圖所示的直角坐標系,過點
為原點建立如圖所示的直角坐標系,過點![]() 作
作![]() ⊥
⊥![]() 軸于點
軸于點![]() ,
,![]() ⊥
⊥![]() 軸于點
軸于點![]() .
.
![]()
![]() =
=![]() =
=![]() ∴
∴![]() =
=![]()
∵點![]() 在正方形對角線
在正方形對角線![]() 上 ∴
上 ∴![]() 點的坐標為
點的坐標為![]()
∴ 過點![]() (0,4),
(0,4),![]() (
(![]() 兩點的函數關系式為:
兩點的函數關系式為:![]()
當![]() 時,
時,![]() ∴
∴![]() 點的坐標為(2,0)
點的坐標為(2,0)
∴![]() 時,△
時,△![]() 的面積是正方形
的面積是正方形![]() 面積的
面積的![]() .
.
(3)若△![]() 是等腰三角形,則有
是等腰三角形,則有 ![]() =
=![]() 或
或![]() =
=![]() 或
或![]() =
=![]()
①當點![]() 運動到與點
運動到與點![]() 重合時,由四邊形
重合時,由四邊形![]() 是正方形知
是正方形知 ![]() =
=![]()
此時△![]() 是等腰三角形
是等腰三角形
②當點![]() 與點
與點![]() 重合時,點
重合時,點![]() 與點
與點![]() 也重合,
也重合,
此時![]() =
=![]() , △
, △![]() 是等腰三角形
是等腰三角形
③解法一:如圖,設點![]() 在
在![]() 邊上運動到
邊上運動到![]() 時,有
時,有![]() =
=![]()
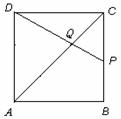
∵ ![]() ∥
∥![]() ∴∠
∴∠![]() =∠
=∠![]()
又∵∠![]() =∠
=∠![]() ∠
∠![]() =∠
=∠![]()
∴∠![]() =∠
=∠![]()
∴ ![]() =
=![]() =
=![]()
∵![]() =
=![]()
![]() =
= ![]() =4
=4
∴![]()
即當![]() 時,△
時,△![]() 是等腰三角形
是等腰三角形
解法二:以![]() 為原點建立如圖所示的直角坐標系,設點
為原點建立如圖所示的直角坐標系,設點![]() 在
在![]() 上運動到
上運動到![]() 時,
時,
有![]() =
=![]() .
.
過點![]() 作
作![]() ⊥
⊥![]() 軸于點
軸于點![]() ,
,![]() ⊥
⊥![]() 軸于點
軸于點![]() ,則
,則![]()
在![]() △
△![]() 中,
中,![]() ,∠
,∠![]() =45°
=45°
∴![]() =
=![]() °=
°=![]()
∴![]() 點的坐標為(
點的坐標為(![]() ,
,![]() )
)
∴過![]() 、
、![]() 兩點的函數關系式:
兩點的函數關系式:![]() +4
+4
當![]() =4時,
=4時,![]() ∴
∴![]() 點的坐標為(4,8-4
點的坐標為(4,8-4![]() ).
).
∴當點![]() 在
在![]() 上運動到
上運動到![]() 時,△
時,△![]() 是等腰三角形.
是等腰三角形.


科目:初中數學 來源: 題型:
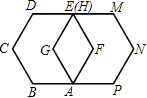 如圖,如果邊長為1的正六邊形ABCDEF繞著頂點A順時針旋轉60°后與正六邊形AGHMNP重合,那么點B的對應點是點
如圖,如果邊長為1的正六邊形ABCDEF繞著頂點A順時針旋轉60°后與正六邊形AGHMNP重合,那么點B的對應點是點查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,將邊長為3的正六邊形A1A2A3A4A5A6,在直線l上由圖1的位置按順時針方向向右作無滑動滾動,當A1第一次滾動到圖2位置時,頂點A1所經過的路徑的長為( )
如圖,將邊長為3的正六邊形A1A2A3A4A5A6,在直線l上由圖1的位置按順時針方向向右作無滑動滾動,當A1第一次滾動到圖2位置時,頂點A1所經過的路徑的長為( )查看答案和解析>>
科目:初中數學 來源:初三數學圓及旋轉題庫 第8講:弧長和扇形面積(解析版) 題型:解答題
 長為半徑作
長為半徑作 ,
, ,
, ,求陰影部分的面積.
,求陰影部分的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com