
【題目】如圖,在![]() 中,
中,![]() ,點
,點![]() 、
、![]() 分別是邊
分別是邊![]() 、
、![]() 的中點,延長
的中點,延長![]() 至
至![]() ,使得
,使得![]() ,連接
,連接![]() 、
、![]() .
.

(1)求證:四邊形![]() 是菱形;
是菱形;
(2)當![]() ,
,![]() 時,判斷
時,判斷![]() 的形狀,并說明理由.
的形狀,并說明理由.
【答案】(1)詳見解析;(2)![]() 是底角為
是底角為![]() 的等腰三角形,解析解析
的等腰三角形,解析解析
【解析】
(1)由“ASA“可證△AEF≌△CED,可得AF=CD,根據鄰邊相等的平行四邊形是菱形即可證明;
(2)由勾股定理可求AB的長,由中位線定理可求DF=DB=5,即可求解.
(1)∵AF∥CD,
∴∠EAF=∠ECD,
∵E是AC中點,
∴AE=EC,
在△AEF和△CED中,
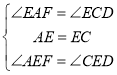
∴△AEF≌△CED(ASA),
∴AF=CD,
∴四邊形AFCD是平行四邊形,
∵∠ACB=![]() ,AD=DB,
,AD=DB,
∴CD=AD=BD,
∴四邊形AFCD是菱形.
(2)∵∠ACB=![]() ,AC=
,AC=![]() ,BC=5,
,BC=5,
∴AB=![]()
∵點D,E分別是邊AB,AC的中點,
∴BC=2DE,DB=![]() AB=5,
AB=5,
∵四邊形AFCD是菱形,
∴DF=2DE=BC=5,
∴DF=DB,
∴△DFB是等腰三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,在矩形OABC中,OA=6,OC=4,F是AB上的一個動點(F不與A,B重合),過點F的反比例函數 ![]() 的圖象與BC邊交于點E.
的圖象與BC邊交于點E.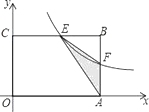
(1)當F為AB的中點時,求該函數的解析式;
(2)當k為何值時,△EFA的面積最大,最大面積是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解:
(1)有理化因式:兩個含有根式的非零代數式相乘,如果它們的積不含有根式,那么這兩個代數式相互叫做有理化因式.例如:![]() 的有理化因式是
的有理化因式是![]() ;
;![]() 的有理化因式是
的有理化因式是![]() .
.
(2)分母有理化:分母有理化又稱“有理化分母”,也就是把分母中的根號化去.指的是如果代數式中分母有根號,那么通常將分子、分母同乘以分母的有理化因式,達到去分母中根號的目的.如:![]() ,
,![]()
問題解決:
(1)填空:![]() 的有理化因式是______.(x≥1)
的有理化因式是______.(x≥1)
(2)直接寫出下列各式分母有理化的結果:
①![]() _____;②
_____;②![]() ______.
______.
(3)計算:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小亮家與姥姥家相距24km,小亮8:00從家出發,騎自行車去姥姥家![]() 媽媽8:30從家出發,乘車沿相同路線去姥姥家
媽媽8:30從家出發,乘車沿相同路線去姥姥家![]() 在同一直角坐標系中,小亮和媽媽的行進路程與北京時間的函數圖象如圖所示,根據圖象得到如下結論,其中錯誤的是
在同一直角坐標系中,小亮和媽媽的行進路程與北京時間的函數圖象如圖所示,根據圖象得到如下結論,其中錯誤的是![]()
![]()
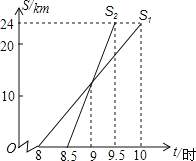
A. 9:00媽媽追上小亮B. 媽媽比小亮提前到達姥姥家
C. 小亮騎自行車的平均速度是![]() D. 媽媽在距家13km處追上小亮
D. 媽媽在距家13km處追上小亮
查看答案和解析>>
科目:初中數學 來源: 題型:
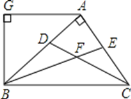
【題目】如圖,AB⊥AC,CD、BE分別是△ABC的角平分線,AG∥BC,AG⊥BG,下列結論:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°.其中正確的結論是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若兩個一次函數與![]() 軸的交點關于
軸的交點關于![]() 軸對稱,則稱這兩個一次函數為“對心函數”,這兩個與
軸對稱,則稱這兩個一次函數為“對心函數”,這兩個與![]() 軸的交點為“對心點”.
軸的交點為“對心點”.

(1)寫出一個![]() 的對心函數:________,這兩個“對心點”為:_______;
的對心函數:________,這兩個“對心點”為:_______;
(2)直線![]() 經過點
經過點![]() 和
和![]() ,直線
,直線![]() 的“對心函數”直線
的“對心函數”直線![]() 與
與![]() 軸的交點
軸的交點![]() 位于點
位于點![]() 的上方,且直線
的上方,且直線![]() 與直線
與直線![]() 交于點
交于點![]() ,點
,點![]() 為直線
為直線![]() 的“對心點”.點
的“對心點”.點![]() 是動直線
是動直線![]() 上不與
上不與![]() 重合的一個動點,且
重合的一個動點,且![]() ,試探究
,試探究![]() 與
與![]() 之間的數量關系,并說明理由.
之間的數量關系,并說明理由.
(3)如圖,直線![]() 與其“對心函數”直線
與其“對心函數”直線![]() 的交點
的交點![]() 位于第一象限,
位于第一象限,![]() 、
、![]() 分別為直線
分別為直線![]() 、
、![]() 的“對心點”,點
的“對心點”,點![]() 為線段
為線段![]() 上一點(不含端點),連接
上一點(不含端點),連接![]() ;一動點
;一動點![]() 從
從![]() 出發,沿線段
出發,沿線段![]() 以
以![]() 單位
單位![]() 秒的速度運動到點
秒的速度運動到點![]() ,再沿線段
,再沿線段![]() 以
以![]() 單位
單位![]() 秒的速度運動到點
秒的速度運動到點![]() 后停止,點
后停止,點![]() 在整個運動過程中所用最短時間為
在整個運動過程中所用最短時間為![]() 秒,求直線
秒,求直線![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校舉辦的”中國漢字聽寫大會“比賽受到各班的廣泛關注,為了了解學生對”中國漢字聽寫大會“活動的喜愛程度,對部分學生進行了隨機抽樣調查,并繪制出如圖所示的兩幅統計圖.在條形圖中,從左向右依次為A類(非常喜歡),B類(較喜歡),C類(一般),D類(不喜歡).請結合兩幅統計圖,回答下列問題
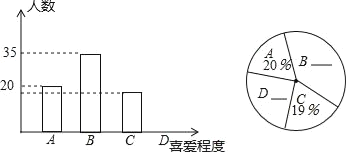
(1)寫出本次抽樣調查的總人數;
(2)請補全兩幅統計圖,寫出計算過程;
(3)若該校有1500名學生.請你估計對“中國漢字聽寫大會”此項活動不喜歡的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校準備為七年級同學慶祝最后一個“兒童節”,至少需要甲種鮮花266朵,乙種鮮花169朵,制成A、B兩種造型共16束.要求A造型用甲種鮮花18朵,乙種鮮花10朵;B造型用甲種鮮花16朵,乙種鮮花11朵,送某花店制作.
(1)花店共有幾種制作方案?分別有哪幾種?
(2)若A種造型每束鮮花可獲得利潤12元,B種造型每束鮮花可獲得利潤10元.如果你是店主,你選擇哪種制作方案?說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com