
【題目】已知在![]() 中,
中,![]() 是
是![]() 的中點,
的中點,![]() ,垂足為
,垂足為![]() ,交
,交![]() 于點
于點![]() ,且
,且![]() .
.
(1)求![]() 的度數;
的度數;
(2)若![]() ,
,![]() ,求
,求![]() 的長.
的長.
【答案】(1)90°(2)1.4
【解析】
(1)連接CE,根據線段垂直平分線的性質轉化線段BE到△AEC中,利用勾股定理的逆定理可求∠A度數;
(2)設AE=x,則AC可用x表示,在Rt△ABC中利用勾股定理得到關于x的方程求解AE值.
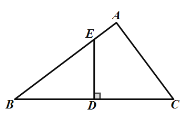
(1)連接CE,∵D是BC的中點,DE⊥BC,
∴CE=BE.
∵BE2AE2=AC2,
∴AE2+AC2=CE2.
∴△AEC是直角三角形,∠A=90°;
(2)在Rt△BDE中,BE=![]() =5.
=5.
所以CE=BE=5.
設AE=x,則在Rt△AEC中,AC2=CE2AE2,
所以AC2=25x2.
∵BD=4,
∴BC=2BD=8.
在Rt△ABC中,根據BC2=AB2+AC2,
即64=(5+x)2+25x2,
解得x=1.4.
即AE=1.4.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖1,直線![]() 分別與y軸、x軸交于點A、點B,點C的坐標為(-3,0),D為直線AB上一動點,連接CD交y軸于點E.
分別與y軸、x軸交于點A、點B,點C的坐標為(-3,0),D為直線AB上一動點,連接CD交y軸于點E.
(1) 點B的坐標為__________,不等式![]() 的解集為___________
的解集為___________
(2) 若S△COE=S△ADE,求點D的坐標;
(3) 如圖2,以CD為邊作菱形CDFG,且∠CDF=60°.當點D運動時,點G在一條定直線上運動,請求出這條定直線的解析式.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠生產某種產品,每件產品的生產成本為25元,出廠價為50元.在生產過程中,平均每生產一件這種產品有0.5m3的污水排出.為凈化環境,該廠購買了一套污水處理設備,每處理1m3污水所需原材料費為2元,每月排污設備耗費4000元.
(1)請給出該廠每月的利潤與產品件數的函數關系式;
(2)為保證每月盈利30000元,該廠每月至少需生產并銷售這種產品多少件?
查看答案和解析>>
科目:初中數學 來源: 題型:
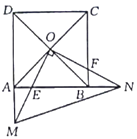
【題目】如圖,正方形![]() 的對角線交于點
的對角線交于點![]() 點
點![]() ,
,![]() 分別在
分別在![]() ,
,![]() 上(
上(![]() )且
)且![]() ,
,![]() ,
,![]() 的延長線交于點
的延長線交于點![]() ,
,![]() ,
,![]() 的延長線交于點
的延長線交于點![]() ,連接
,連接![]() .
.
(1)求證:![]() .
.
(2)若正方形![]() 的邊長為4,
的邊長為4,![]() 為
為![]() 的中點,求
的中點,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
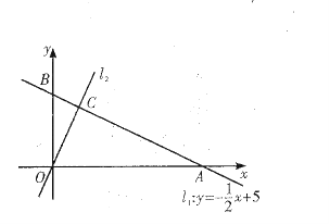
【題目】如圖,在平面直角坐標系![]() 中,一次函數
中,一次函數![]() 的圖象
的圖象![]() 分別與
分別與![]() 軸交于
軸交于![]() 兩點,正比例函數的圖象
兩點,正比例函數的圖象![]() 與
與![]() 交于點
交于點![]()
(1)求![]() 的值及
的值及![]() 的解析式;
的解析式;
(2)求![]() 的值;
的值;
(3)一次函數![]() 的圖象為
的圖象為![]() 且
且![]() 不能圍成三角形,直接寫出
不能圍成三角形,直接寫出![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的布袋中有2個紅球和3個黑球,它們只有顏色上的區別.
(1)從布袋中隨機摸出一個球,求摸出紅球的概率;
(2)現從布袋中取出一個紅球和一個黑球,放入另一個不透明的空布袋中,甲乙兩人約定做如下游戲:兩人分別從這兩個布袋中各隨機摸出一個小球,若顏色相同,則甲獲勝;若顏色不同,則乙獲勝.請用樹狀圖(或列表)的方法表示游戲所有可能的結果,并用概率知識說明這個游戲是否公平?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】新農村社區改造中,有一部分樓盤要對外銷售.某樓盤共23層,銷售價格如下:第八層樓房售價為4000元/米2 , 從第八層起每上升一層,每平方米的售價提高50元;反之,樓層每下降一層,每平方米的售價降低30元.已知該樓盤每套樓房面積均為120米2 , 若購買者一次性付清所有房款,開發商有兩種優惠方案:
方案一:降價8%,另外每套樓房贈送a元裝修基金;
方案二:降價l0%,沒有其他贈送.
(1)請寫出售價y(元/米2)與樓層x( ![]() ,x取整數)之間的函數關系式;
,x取整數)之間的函數關系式;
(2)老王要購買第十六層的一套樓房,若他一次性付清購房款,請幫他計算哪種優惠方案更加合算.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將一列有理數﹣1,2,﹣3,4,﹣5,6,……,如圖所示有序排列.根據圖中的排列規律可知,“峰1”中峰頂的位置(C的位置)是有理數4,那么,“峰6”中C的位置是有理數_____,2018應排在A,B,C,D,E中的_____位置.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com