
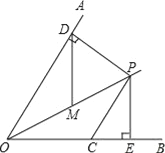
【題目】如圖,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于點D,PE⊥OB于點E.如果點M是OP的中點,則DM的長是( )
A. 2 B. ![]() C.
C. ![]() D. 2
D. 2![]()
【答案】C
【解析】試題分析:由OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,易得△OCP是等腰三角形,∠COP=30°,又由含30°角的直角三角形的性質,即可求得PE的值,繼而求得OP的長,然后由直角三角形斜邊上的中線等于斜邊的一半,即可求得DM的長.
解:∵OP平分∠AOB,∠AOB=60°,
∴∠AOP=∠COP=30°,
∵CP∥OA,
∴∠AOP=∠CPO,
∴∠COP=∠CPO,
∴OC=CP=2,
∵∠PCE=∠AOB=60°,PE⊥OB,
∴∠CPE=30°,
∴CE=![]() CP=1,
CP=1,
∴PE=![]() =
=![]() ,
,
∴OP=2PE=2![]() ,
,
∵PD⊥OA,點M是OP的中點,
∴DM=![]() OP=
OP=![]() .
.
故選:C.


 怎樣學好牛津英語系列答案
怎樣學好牛津英語系列答案科目:初中數學 來源: 題型:
【題目】我們知道:任意一個有理數與無理數的和為無理數,任意一個不為零的有理數與一個無理數的積為無理數,而零與無理數的積為零.由此可得:如果ax+b=0,其中a、b為有理數,x為無理數,那么a=0且b=0.
運用上述知識,解決下列問題:
(1)如果(a+2) ![]() -b+3=0,其中a、b為有理數,那么a= , b=;
-b+3=0,其中a、b為有理數,那么a= , b=;
(2)如果2b-a-(a+b-4) ![]() =5,其中a、b為有理數,求3a+2b的平方根.
=5,其中a、b為有理數,求3a+2b的平方根.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列四組線段中,可以構成直角三角形的是( )
A.4cm、5cm、6cm
B.1cm、 ![]() cm、3cm
cm、3cm
C.2cm、3cm、4cm
D.1.5cm、2cm、2.5cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,一次函數y=ax+b(a≠0)的圖形與反比例函數y=![]() (k≠0)的圖象交于第二、四象限內的A、B兩點,與y軸交于C點,過點A作AH⊥y軸,垂足為H,OH=3,tan∠AOH=
(k≠0)的圖象交于第二、四象限內的A、B兩點,與y軸交于C點,過點A作AH⊥y軸,垂足為H,OH=3,tan∠AOH=![]() ,點B的坐標為(m,﹣2).
,點B的坐標為(m,﹣2).
(1)求△AHO的周長;
(2)求該反比例函數和一次函數的解析式.

查看答案和解析>>
科目:初中數學 來源: 題型:
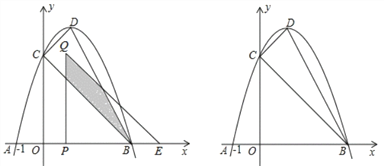
【題目】如圖,拋物線y=﹣(x﹣1)2+c與x軸交于A,B(A,B分別在y軸的左右兩側)兩點,與y軸的正半軸交于點C,頂點為D,已知A(﹣1,0).
(1)求點B,C的坐標;
(2)判斷△CDB的形狀并說明理由;
(3)將△COB沿x軸向右平移t個單位長度(0<t<3)得到△QPE.△QPE與△CDB重疊部分(如圖中陰影部分)面積為S,求S與t的函數關系式,并寫出自變量t的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com