
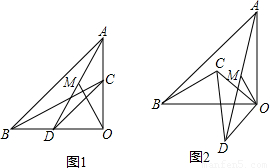
 DF,再由∠AOB=∠BOF=∠COD=90°,得出∠COB=∠DOF,根據SAS判斷△COB≌△DOF,則DF=BC,所以MO=
DF,再由∠AOB=∠BOF=∠COD=90°,得出∠COB=∠DOF,根據SAS判斷△COB≌△DOF,則DF=BC,所以MO= BC;
BC;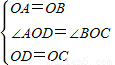
 BC.
BC.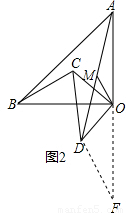 證明:延長AO到F,使FO=AO.連接DF,
證明:延長AO到F,使FO=AO.連接DF, DF,
DF,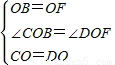 ,
, BC;
BC;

科目:初中數學 來源: 題型:
| 3 |
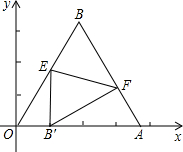 正方向上,將△OAB折疊,使點B落在邊OA上,記為B′,折痕為EF.
正方向上,將△OAB折疊,使點B落在邊OA上,記為B′,折痕為EF.查看答案和解析>>
科目:初中數學 來源: 題型:
 (2008•武漢模擬)如圖所示,△OAB,△OCD為等腰直角三角形,∠AOB=∠COD=90°.
(2008•武漢模擬)如圖所示,△OAB,△OCD為等腰直角三角形,∠AOB=∠COD=90°.查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖所示,△OAB繞點O旋轉l80°得到△OCD,連接AD,BC,得到四邊形ABCD.
如圖所示,△OAB繞點O旋轉l80°得到△OCD,連接AD,BC,得到四邊形ABCD.查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖所示,△OAB是邊長為2+
如圖所示,△OAB是邊長為2+| 3 |
查看答案和解析>>
科目:初中數學 來源:2013年廣東省汕尾市中考數學模擬試卷(一)(解析版) 題型:解答題
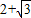 的等邊三角形,其中O是坐標原點,頂點A在x軸的正方向上,將△OAB折疊,使點B落在邊OA上,記為B′,折痕為EF.
的等邊三角形,其中O是坐標原點,頂點A在x軸的正方向上,將△OAB折疊,使點B落在邊OA上,記為B′,折痕為EF.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com