
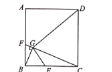
【題目】如圖,在正方形![]() 中,
中,![]() 分別是邊
分別是邊![]() 上的點,且滿足
上的點,且滿足![]() ,連接
,連接![]() ,過點B作
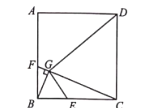
,過點B作![]() ,垂足為點G,連接DG,則下列說法不正確的是( )
,垂足為點G,連接DG,則下列說法不正確的是( )
A.![]() B.
B.![]() C.
C.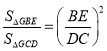 D.
D.![]()
【答案】B
【解析】
根據正方形的性質、等角的余角相等即可判斷A正確;根據B選項,判斷出E為BC中點,與原題條件不一致,判斷B錯誤;證明![]() ,判斷C選項正確;根據
,判斷C選項正確;根據![]() ,得出
,得出![]() ,判斷D正確.
,判斷D正確.
解:![]() 四邊形
四邊形![]() 是正方形,
是正方形,
![]() ,即
,即![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() 選項正確,不合題意;
選項正確,不合題意;
∵BG⊥CF,
∴∠BGC=90°,
∴∠GBC+∠BCG=90°, ∠BGE+∠CGE=90°,
當GE=BE時,∠BGE=∠GBE,
∴∠EGC=∠ECG,
∴GE=CE,
∴BE=CE,
即E為BC中點,
原題沒有此條件,∴B選項不正確,符合題意;
![]() ,
,![]() ,
,
∴∠FBG+∠CBG=90°, ∠FBG+∠BFG=90°,
∴∠CBG=∠BFG,
![]() ,
,
![]()
![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() ,又
,又![]() ,
,
![]() ,
,
![]()
![]() ,
,
∴![]() 選項正確,不合題意;
選項正確,不合題意;
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
∴![]() 選項正確,不合題意;
選項正確,不合題意;
故選:![]() .
.


科目:初中數學 來源: 題型:
【題目】為了解某校九年級學生的理化實驗操作情況,隨機抽查了40名同學實驗操作的得分,根據獲取的樣本數據,制作了如下的條形統計圖和扇形統計圖.請根據相關信息,解答下列問題:
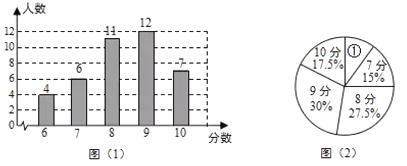
(1)①中的描述應為“6分![]() ”,其中
”,其中![]() 的值為 ;扇形①的圓心角的大小是 ;
的值為 ;扇形①的圓心角的大小是 ;
(2)求這40個樣本數據的平均數、眾數、中位數;
(3)若該校九年級共有360名學生,估計該校理化實驗操作得滿分的學生有多少人.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下表:
序號 | 1 | 2 | 3 | … |
圖形 |
|
|
| … |
我們把某格中字母和所得到的多項式稱為特征多項式,例如:
第1格的“特征多項式”為![]() ;
;
第2格的“特征多項式”為![]() .
.
回答下列問題:
(1)第3格的“特征多項式”為________________,
第4格的“特征多項式”為______________________,
第![]() 格的“特征多項式”為___________________;
格的“特征多項式”為___________________;
(2)若第1格的“特征多項式”的值為![]() ,第2格的“特征多項式”的值為
,第2格的“特征多項式”的值為![]() ,求
,求![]() 的值;
的值;
(3)在(2)的條件下,第![]() 格的特征多項式的值為
格的特征多項式的值為![]() ,則直接寫出
,則直接寫出![]() 的值;若沒有,請說明理由.
的值;若沒有,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
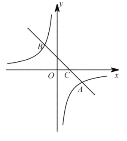
【題目】如圖,在平面直角坐標系中,一次函數![]() 的圖像與反比例函數
的圖像與反比例函數![]() 的圖像交與A(4,-2),B(-2,n)兩點,與
的圖像交與A(4,-2),B(-2,n)兩點,與![]() 軸交與點C.
軸交與點C.
(1)求![]() ,n的值;
,n的值;
(2)請直接寫出不等式![]() 的解集;
的解集;
(3)點A關于![]() 軸對稱得到點A’,連接A’B,A’C,求△A’BC的面積.
軸對稱得到點A’,連接A’B,A’C,求△A’BC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某種雜交柑橘新品種,皮薄汁多,口感細嫩,風味極佳,深受怎么喜愛,某果農種植銷售過程中發現,這種柑橘的種植成本為6元/千克,日銷量![]() 與銷售單價
與銷售單價![]() (元)之間存在一次函數關系,如圖所示
(元)之間存在一次函數關系,如圖所示
(1)求![]() 與
與![]() 之間的函數關系式
之間的函數關系式
(2)該果農每天銷售這種柑橘不低于60千克且不超過150千克,試求其銷售單價定為多少時,除去種植成本后,每天銷售利潤最大?最大利潤是多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
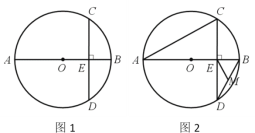
【題目】已知AB是⊙O的直徑,C是⊙O上的一點(不與點A,B重合),過點C作AB的垂線交⊙O于點D,垂足為E點.
(1)如圖1,當AE=4,BE=2時,求CD的長度;
(2)如圖2,連接AC,BD,點M為BD的中點.求證:ME⊥AC.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】襄陽市精準扶貧工作已進入攻堅階段.貧困戶張大爺在某單位的幫扶下,把一片坡地改造后種植了優質水果藍莓,今年正式上市銷售.在銷售的30天中,第一天賣出20千克,為了擴大銷量,采取了降價措施,以后每天比前一天多賣出4千克.第x天的售價為y元/千克,y關于x的函數解析式為![]() 且第12天的售價為32元/千克,第26天的售價為25元/千克.已知種植銷售藍莓的成木是18元/千克,每天的利潤是W元(利潤=銷售收入﹣成本).
且第12天的售價為32元/千克,第26天的售價為25元/千克.已知種植銷售藍莓的成木是18元/千克,每天的利潤是W元(利潤=銷售收入﹣成本).
(1)m= ,n= ;
(2)求銷售藍莓第幾天時,當天的利潤最大?最大利潤是多少?
(3)在銷售藍莓的30天中,當天利潤不低于870元的共有多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
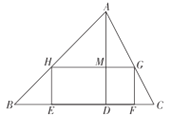
【題目】如圖所示,要在底邊BC=160cm,高AD=120cm的△ABC鐵皮余料上,截取一個矩形EFGH,使點H在AB上,點G在AC上,點E,F在BC上,AD交HG于點M.
(1)設矩形EFGH的長HG=ycm,寬HE=xcm.求y與x的函數關系式;
(2)當x為何值時,矩形EFGH的面積S最大?最大值是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com