
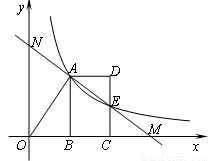
如圖,反比例函數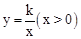 的圖象經過線段OA的端點A,O為原點,作AB⊥x軸于點B,點B的坐標為(2,0),tan∠AOB=
的圖象經過線段OA的端點A,O為原點,作AB⊥x軸于點B,點B的坐標為(2,0),tan∠AOB=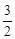 。
。
(1)求k的值;
(2)將線段AB沿x軸正方向平移到線段DC的位置,反比例函數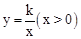 的圖象恰好經過DC的中點E,求直線AE的函數表達式;
的圖象恰好經過DC的中點E,求直線AE的函數表達式;
(3)若直線AE與x軸交于點M、與y軸交于點N,請你探索線段AN與線段ME的大小關系,寫出你的結論并說明理由.
解:(1)由已知條件得,在Rt△OAB中,OB=2,tan∠AOB=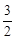 ,∴
,∴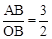 。∴AB=3。
。∴AB=3。
∴A點的坐標為(2,3)。
∴k=xy=6。
(2)∵DC由AB平移得到,點E為DC的中點,∴點E的縱坐標為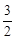 。
。
又∵點E在雙曲線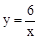 上,∴點E的坐標為(4,
上,∴點E的坐標為(4,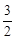 )。
)。
設直線AE的函數表達式為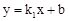 ,則
,則
 ,解得
,解得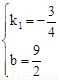 。
。
∴直線AE的函數表達式為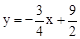 。
。
(3)結論:AN=ME。理由:
在表達式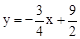 中,令y=0可得x=6,令x=0可得y=
中,令y=0可得x=6,令x=0可得y=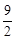 。
。
∴點M(6,0),N(0,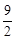 )。
)。
解法一:延長DA交y軸于點F,則AF⊥ON,且AF=2,OF=3,
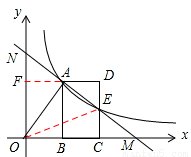
∴NF=ON-OF=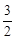 。
。
∴根據勾股定理可得AN=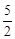 。
。
∵CM=6-4=2,EC=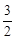 ,
,
∴根據勾股定理可得EM=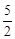 。
。
∴AN=ME。
解法二:連接OE,延長DA交y軸于點F,則AF⊥ON,且AF=2,
∵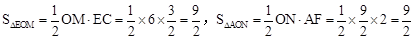 ,
,
∴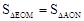 ,
,
∵AN和ME邊上的高相等,
∴AN=ME。
【解析】
試題分析:(1)在直角△AOB中利用三角函數求得A的坐標,然后利用待定系數法即可求得k的值.
(2)已知E是DC的中點,則E的縱坐標已知,代入反比例函數的解析式即可求得E的坐標,然后利用待定系數法即可求得直線的解析式.
(3)首先求得M、N的坐標,延長DA交y軸于點F,則AF⊥ON,利用勾股定理求得AN和EM的長,即可證得.


科目:初中數學 來源: 題型:
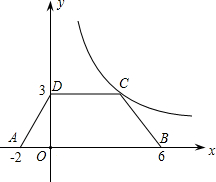 (2012•南昌)如圖,等腰梯形ABCD放置在平面坐標系中,已知A(-2,0)、B(6,0)、D(0,3),反比例函數的圖象經過點C.
(2012•南昌)如圖,等腰梯形ABCD放置在平面坐標系中,已知A(-2,0)、B(6,0)、D(0,3),反比例函數的圖象經過點C.查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•和平區一模)如圖,反比例函數的圖象經過點A、B,點A的坐標為(1,3),點B的縱坐標為1,點C的坐標為(2,0).
(2013•和平區一模)如圖,反比例函數的圖象經過點A、B,點A的坐標為(1,3),點B的縱坐標為1,點C的坐標為(2,0).查看答案和解析>>
科目:初中數學 來源: 題型:
 (2012•湖里區一模)如圖,反比例函數y=
(2012•湖里區一模)如圖,反比例函數y=| k |
| x |
| k |
| x |
查看答案和解析>>
科目:初中數學 來源: 題型:
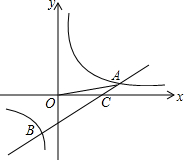 已知:如圖,反比例函數的圖象和一次函數的圖象交于A和B兩點,且點A的坐標為(3,1),點B的坐標為(-1,-3),一次函數圖象與X軸交于點C.連接OA.
已知:如圖,反比例函數的圖象和一次函數的圖象交于A和B兩點,且點A的坐標為(3,1),點B的坐標為(-1,-3),一次函數圖象與X軸交于點C.連接OA.查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,反比例函數![]() 的圖象與直線
的圖象與直線![]() 在第一象限交于點
在第一象限交于點![]() ,
,![]() 為直線上的兩點,點
為直線上的兩點,點![]() 的橫坐標為2,點
的橫坐標為2,點![]() 的橫坐標為3.
的橫坐標為3.![]() 為反比例函數圖象上的兩點,且
為反比例函數圖象上的兩點,且![]() 平行于
平行于![]() 軸.
軸.
(1)直接寫出![]() 的值;
的值;
(2)求梯形![]() 的面積.
的面積.
 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com