【題目】解下列方程：
（1）
=3．
（2）（y+2）2=（3y﹣1）2．
（3）（x﹣2）（x+5）=8．
（4）（2x+1）2=﹣6x﹣3．
（5）2x2﹣3x﹣2=0．
（6）4x2﹣12x﹣1=0（配方法）．
【答案】(1) x1=0，x2=﹣6；(2) y1=﹣
，y2=
；(3) x1=3，x2=﹣6；(4) x1=﹣
，x2=﹣2；(5)x1=﹣，x2=2；(6) x1=
，x2=
．
【解析】
（1）變形后開方，即可得出兩個一元一次方程，求出方程的解即可；
（2）移項后分解因式，開方，即可得出兩個一元一次方程，求出方程的解即可；
（3）整理后分解因式，即可得出兩個一元一次方程，求出方程的解即可；
（4）移向后分解因式，即可得出兩個一元一次方程，求出方程的解即可；
（5）先分解因式，即可得出兩個一元一次方程，求出方程的解即可；
（6）移項，系數化成1，配方，開方，即可得出兩個一元一次方程，求出方程的解即可．
（1）
=3，
（x+3）2=9，
x+3=±3，
x1=0，x2=﹣6；
（2）（y+2）2=（3y﹣1）2．
（y+2）2﹣（3y﹣1）2，=0，
[（y+2）+（3y﹣1）][（y+2）﹣（3y﹣1）]=0，
（y+2）+（3y﹣1）=0，（y+2）﹣（3y﹣1）=0，
y1=﹣
，y2=
；
（3）（x﹣2）（x+5）=8．
整理得：x2+3x﹣18=0，
（x﹣3）（x+6）=0，
x﹣3=0，x+6=0，
x1=3，x2=﹣6；
（4）（2x+1）2=﹣6x﹣3，
（2x+1）2+3（2x+1）=0，
（2x+1）（2x+1+3）=0，
2x+1=0，2x+1+3=0，
x1=﹣
，x2=﹣2；
（5）2x2﹣3x﹣2=0，
（2x+1）（x﹣2）=0，
2x+1=0，x﹣2=0，
x1=﹣，x2=2；
（6）4x2﹣12x﹣1=0
4x2﹣12x=1，
x2﹣3x+（）2=
+（
）2，
（x﹣）2=
，
x﹣=±
，
x1=
，x2=
．
科目：初中數學 來源： 題型：
【題目】如圖，一架云梯AB的長25 m，斜靠在一面墻上，梯子靠墻的一端A距地面距離AC為24 m．
(1)這個梯子底端B離墻的距離BC有多少米？
(2)如果梯子的頂端下滑了4 m，那么梯子的底部在水平方向也滑動了4 m嗎？為什么？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AB，BC，CD分別與⊙O相切于E，F，G．且AB∥CD．BO=6cm，CO=8cm． 
（1）求證：BO⊥CO；
（2）求BE和CG的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
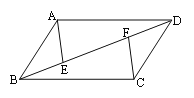
【題目】如圖，四邊形ABCD中，AB＝CD，AB∥CD，點E、F在線段BD上，且BE＝DF，連接AE、CF．
（1）指出線段AE與CF的關系，并說明理由；
（2）若將題中的條件“點E、F在線段BD上”改為“點E、F在直線BD上” ，那么(1)中的結論還一定能成立嗎？若能，直接寫出結論；若不能，請舉出反例加以說明．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】【問題情境】
課外興趣小組活動時，老師提出了如下問題：
如圖①，△ABC中，若AB＝12，AC＝8，求BC邊上的中線AD的取值范圍．
小明在組內經過合作交流，得到了如下的解決方法：延長AD至點E，使DE＝AD，連接BE．請根據小明的方法思考：
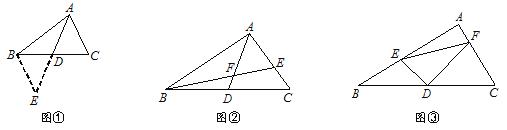
（1）由已知和作圖能得到△ADC≌△EDB，依據是 ．
A．SSS B．SAS C．AAS D．HL
（2）由“三角形的三邊關系”可求得AD的取值范圍是 ．
解后反思：題目中出現“中點”、“中線”等條件，可考慮延長中線構造全等三角形，把分散的已知條件和所求證的結論集中到同一個三角形之中．
【初步運用】
如圖②，AD是△ABC的中線，BE交AC于E，交AD于F，且AE＝EF．若EF＝3，EC＝2，求線段BF的長．
【靈活運用】
如圖③，在△ABC中， ∠A＝90°，D為BC中點， DE⊥DF，DE交AB于點E，DF交AC于點F，連接EF．試猜想線段BE、CF、EF三者之間的等量關系，并證明你的結論．
查看答案和解析>>
科目：初中數學 來源： 題型：
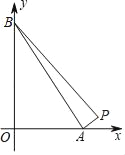
【題目】由點P（14，1），A（a，0），B（0，a）確定的△PAB的面積為18．
（1）如圖，若0＜a＜14，求a的值．
（2）如果a＞14，請畫圖并求a的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，∠ABE=∠ACD=Rt∠，AE=AD，∠ABC=∠ACB.求證：∠BAE=∠CAD．
請補全證明過程，并在括號里寫上理由．
證明：在△ABC中，
∵∠ABC=∠ACB
∴AB= （ ）
在Rt△ABE和Rt△ACD中，
∵ =AC， =AD
∴Rt△ABE≌Rt△ACD（ ）
∴∠BAE=∠CAD（ ）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在菱形ABCD中，AB=2 
，∠C=120°，以點C為圓心的 
與AB，AD分別相切于點G，H，與BC，CD分別相交于點E，F．若用扇形CEF作一個圓錐的側面，則這個圓錐的高是 ． 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
