【答案】
分析:(1)根據一次函數圖象的平移問題由y=

x的圖象向下平移6個單位得到直線BC的解析式為y=

x-6,然后把y=0代入即可確定C點坐標;
(2)作AE⊥x軸于E點,BF⊥x軸于F點,易證得Rt△OAE∽△RtCBF,則
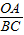
=
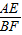
=
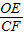
=2,若設A點坐標為(a,

a),則CF=

a,BF=

a,得到B點坐標為(

+

a,

a),然后根據反比例函數上點的坐標特征得a•

a=(

+

a)•

a,解得a=3,于是可確定點A的坐標為(3,4),再利用待定系數法確定反比例函數的解析式.
解答:解:(1)∵y=

x的圖象向下平移6個單位后與雙曲線y=

交于點B,與x軸交于點C,
∴直線BC的解析式為y=

x-6,
把y=0代入得

x-6=0,解得x=

,
∴C點坐標為(

,0);
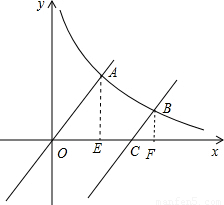
(2)作AE⊥x軸于E點,BF⊥x軸于F點,如圖,
∵OA∥BC,
∴∠AOC=∠BCF,
∴Rt△OAE∽△RtCBF,
∴

=
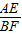
=
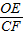
=2,
設A點坐標為(a,

a),則OE=a,AE=

a,
∴CF=

a,BF=

a,
∴OF=OC+CF=

+

a,
∴B點坐標為(

+

a,

a),
∵點A與點B都在y=
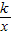
的圖象上,
∴a•

a=(

+

a)•

a,解得a=3,
∴點A的坐標為(3,4),
把A(3,4)代入y=

得k=3×4=12,
∴反比例函數的解析式為y=
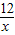
.
點評:本題考查了反比例函數與一次函數的交點問題:反比例函數與一次函數的交點坐標滿足兩函數的解析式.也考查了相似三角形的判定與性質以及一次函數圖象的平移問題.

 x與反比例函數y=
x與反比例函數y= (x>0)的圖象交于點A.將y=
(x>0)的圖象交于點A.將y= x的圖象向下平移6個單位后與雙曲線y=
x的圖象向下平移6個單位后與雙曲線y= 交于點B,與x軸交于點C.
交于點B,與x軸交于點C. =2,求反比例函數的解析式.
=2,求反比例函數的解析式.
 x的圖象向下平移6個單位得到直線BC的解析式為y=
x的圖象向下平移6個單位得到直線BC的解析式為y= x-6,然后把y=0代入即可確定C點坐標;
x-6,然后把y=0代入即可確定C點坐標;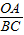 =
=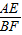 =
=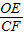 =2,若設A點坐標為(a,
=2,若設A點坐標為(a, a),則CF=
a),則CF= a,BF=
a,BF= a,得到B點坐標為(
a,得到B點坐標為( +
+ a,
a, a),然后根據反比例函數上點的坐標特征得a•
a),然后根據反比例函數上點的坐標特征得a• a=(
a=( +
+ a)•
a)• a,解得a=3,于是可確定點A的坐標為(3,4),再利用待定系數法確定反比例函數的解析式.
a,解得a=3,于是可確定點A的坐標為(3,4),再利用待定系數法確定反比例函數的解析式. x的圖象向下平移6個單位后與雙曲線y=
x的圖象向下平移6個單位后與雙曲線y= 交于點B,與x軸交于點C,
交于點B,與x軸交于點C,
 x-6,
x-6, x-6=0,解得x=
x-6=0,解得x= ,
, ,0);
,0); =
=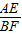 =
=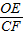 =2,
=2, a),則OE=a,AE=
a),則OE=a,AE= a,
a, a,BF=
a,BF= a,
a, +
+ a,
a, +
+ a,
a, a),
a),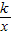 的圖象上,
的圖象上, a=(
a=( +
+ a)•
a)• a,解得a=3,
a,解得a=3, 得k=3×4=12,
得k=3×4=12,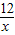 .
.

 如圖,已知函數y1=kx+b與函數y2=
如圖,已知函數y1=kx+b與函數y2= 14、如圖,已知函數y=3x+b和y=ax-3的圖象交于點P(-2,-5),則根據圖象可得不等式3x+b>ax-3的解集在數軸上表示正確的是( )
14、如圖,已知函數y=3x+b和y=ax-3的圖象交于點P(-2,-5),則根據圖象可得不等式3x+b>ax-3的解集在數軸上表示正確的是( )



 如圖,已知函數y=ax+b和y=kx的圖象交于點P,則根據圖象可得,關于
如圖,已知函數y=ax+b和y=kx的圖象交于點P,則根據圖象可得,關于