
如圖10,C是線段AB上的一點(diǎn),△ACD和△BCE都是等邊三角形.
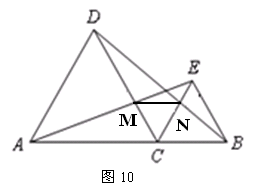
(1)求證:AE=BD;
(2)若AE交CD于M,BD交CE于N,連結(jié)MN,試判斷△MCN的形狀,并說(shuō)明理由.
(1)證明略
(2)等邊三角形,理由略
【解析】(1)證明:∵△ACD和△BCE都是等邊三角形
∴AC=CD,CE=CB,∠ACD=∠BCE=60°…………………………………1分
∵∠ACD+∠DCE=∠BCE+∠DCE
∴∠ACE=∠DCB………………………………………………………………2分
∴△ACE≌△DCB
∴AE=BD…………………………………………………………………………3分
(2)△MCN是等邊三角形…………………………………………………………4分
∵∠ACD=∠BCE=60°,∠ACB是一個(gè)平角
∴∠DCE=60°
即∠ACM=∠DCN…………………………………………………………………5分
由(1)得△ACE≌△DCB
∴∠CAM=∠CDN…………………………………………………………………6分
又AC=DC
∴△ACM≌△DCN…………………………………………………………………7分



 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
如圖10,C是線段AB上的一點(diǎn),△ACD和△BCE都是等邊三角形.
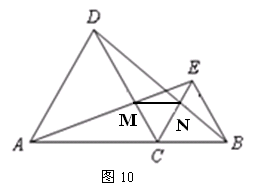
(1)求證:AE=BD;
(2)若AE交CD于M,BD交CE于N,連結(jié)MN,試判斷△MCN的形狀,并說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源:2011年江蘇省姜堰市初一第一學(xué)期期末考試數(shù)學(xué)卷 題型:解答題
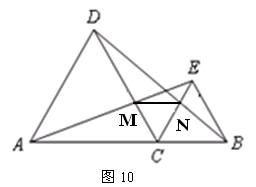
如圖10,C是線段AB上的一點(diǎn),△ACD 和△BCE都是等邊三角形.
和△BCE都是等邊三角形.
 (1)求證:AE=BD;
(1)求證:AE=BD;
(2)若AE交CD于M,BD交CE于N,連結(jié)MN,試判斷△MCN的形狀,并說(shuō)明理由.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com