
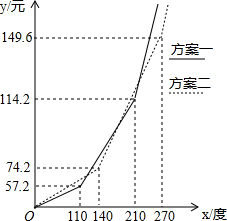
 國家發改委日前表示,居民階梯電價方案將在今年上半年推出,按發改委先前公布的《居民用電實行階梯電價的指導意見(征求意見稿)》的標準,繪制了居民每月電費y(元)隨本月用電量x(度)變化的圖象.根據圖象中的有關數據解答下列問題:
國家發改委日前表示,居民階梯電價方案將在今年上半年推出,按發改委先前公布的《居民用電實行階梯電價的指導意見(征求意見稿)》的標準,繪制了居民每月電費y(元)隨本月用電量x(度)變化的圖象.根據圖象中的有關數據解答下列問題: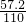 =0.52元;當x≤140時,按方案二,每度電價=
=0.52元;當x≤140時,按方案二,每度電價=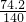 =0.53元;
=0.53元; ,
, ,
, ,
,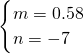 ,
,

 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:初中數學 來源: 題型:
 (2012•南關區模擬)國家發改委日前表示,居民階梯電價方案將在今年上半年推出,按發改委先前公布的《居民用電實行階梯電價的指導意見(征求意見稿)》的標準,繪制了居民每月電費y(元)隨本月用電量x(度)變化的圖象.根據圖象中的有關數據解答下列問題:
(2012•南關區模擬)國家發改委日前表示,居民階梯電價方案將在今年上半年推出,按發改委先前公布的《居民用電實行階梯電價的指導意見(征求意見稿)》的標準,繪制了居民每月電費y(元)隨本月用電量x(度)變化的圖象.根據圖象中的有關數據解答下列問題:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com