
【題目】如圖,BD是正方形ABCD的對角線,BC=2,邊BC在其所在的直線上平移,將通過平移得到的線段記為PQ,連接PA、QD,并過點Q作QO⊥BD,垂足為O,連接OA、OP.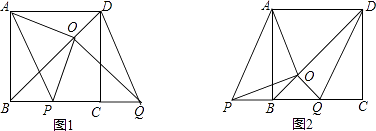
(1)請直接寫出線段BC在平移過程中,四邊形APQD是什么四邊形?
(2)請判斷OA、OP之間的數量關系和位置關系,并加以證明;
(3)在平移變換過程中,設y=S△OPB , BP=x(0≤x≤2),求y與x之間的函數關系式,并求出y的最大值.
【答案】
(1)
四邊形APQD為平行四邊形;
(2)
OA=OP,OA⊥OP,理由如下:
∵四邊形ABCD是正方形,
∴AB=BC=PQ,∠ABO=∠OBQ=45°,
∵OQ⊥BD,
∴∠PQO=45°,
∴∠ABO=∠OBQ=∠PQO=45°,
∴OB=OQ,
在△AOB和△OPQ中,

∴△AOB≌△POQ(SAS),
∴OA=OP,∠AOB=∠POQ,
∴∠AOP=∠BOQ=90°,
∴OA⊥OP;
(3)
過O作OE⊥BC于E.
①如圖1,當P點在B點右側時,
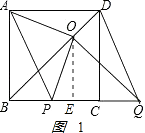
則BQ=x+2,OE= ![]() ,
,
∴y= ![]() ×
× ![]() x,即y=
x,即y= ![]() (x+1)2﹣
(x+1)2﹣ ![]() ,
,
又∵0≤x≤2,
∴當x=2時,y有最大值為2;
②如圖2,當P點在B點左側時,

則BQ=2﹣x,OE= ![]() ,
,
∴y= ![]() ×
× ![]() x,即y=﹣
x,即y=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() ,
,
又∵0≤x≤2,
∴當x=1時,y有最大值為 ![]() ;
;
綜上所述,∴當x=2時,y有最大值為2;
【解析】(1)根據平移的性質,可得PQ,根據一組對邊平行且相等的四邊形是平行四邊形,可得答案;(2)根據正方形的性質,平移的性質,可得PQ與AB的關系,根據等腰直角三角形的判定與性質,可得∠PQOPQO,根據全等三角形的判定與性質,可得AO與OP的數量關系,根據余角的性質,可得AO與OP的位置關系;(3)根據等腰直角三角形的性質,可得OE的長,根據三角形的面積公式,可得二次函數,根據二次函數的性質,可得到答案.


科目:初中數學 來源: 題型:
【題目】現代互聯網技術的廣泛應用,催生了快遞行業的高速發展.小明計劃給朋友快遞一部分物品,經了解有甲、乙兩家快遞公司比較合適.甲公司表示:快遞物品不超過1千克的,按每千克22元收費;超過1千克,超過的部分按每千克15元收費.乙公司表示:按每千克16元收費,另加包裝費3元.設小明快遞物品x千克.
(1)請分別寫出甲、乙兩家快遞公司快遞該物品的費用y(元)與x(千克)之間的函數關系式;
(2)小明選擇哪家快遞公司更省錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
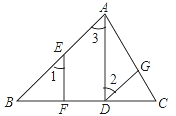
【題目】如圖,已知△ABC中,AD⊥BC于點D,E為AB邊上任意一點,EF⊥BC于點F,∠1=∠2.求證:DG∥AB.請把證明的過程填寫完整.
證明:∵AD⊥BC,EF⊥BC( ),
∴∠EFB=∠ADB=90°(垂直的定義)
∴EF∥ ( )
∴∠1= ( )
又∵∠1=∠2(已知)
∴ ( )
∴DG∥AB( )
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】以下是某省2010年教育發展情況有關數據:
全省共有各級各類學校25000所,其中小學12500所,初中2000所,高中450所,其它學校10050所;全省共有在校學生995萬人,其中小學440萬人,初中200萬人,高中75萬人,其它280萬人;全省共有在職教師48萬人,其中小學20萬人,初中12萬人,高中5萬人,其它11萬人.
請將上述資料中的數據按下列步驟進行統計分析.
(1)整理數據:請設計一個統計表,將以上數據填入表格中.
(2)描述數據:下圖是描述全省各級各類學校所數的扇形統計圖,請將它補充完整.
(3)分析數據:
①分析統計表中的相關數據,小學、初中、高中三個學段的師生比,最小的是哪個學段?請直接寫出.(師生比=在職教師數︰在校學生數)
②根據統計表中的相關數據,你還能從其它角度分析得出什么結論嗎?(寫出一個即可)
③從扇形統計圖中,你得出什么結論?(寫出一個即可)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,直線y=﹣x+3與x軸交于點C,與直線AD交于點A( ![]() ,
, ![]() ),點D的坐標為(0,1)
),點D的坐標為(0,1) 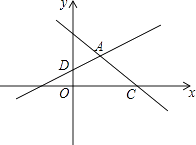
(1)求直線AD的解析式;
(2)直線AD與x軸交于點B,若點E是直線AD上一動點(不與點B重合),當△BOD與△BCE相似時,求點E的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
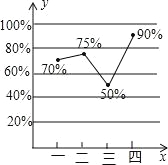
【題目】某汽車廠去年每個季度汽車銷售數量(輛)占當季汽車產量(輛)百分比的統計圖如圖所示.根據統計圖回答下列問題:
(1)若第一季度的汽車銷售量為2100輛,求該季的汽車產量;
(2)圓圓同學說:“因為第二,第三這兩個季度汽車銷售數量占當季汽車產量是從75%降到50%,所以第二季度的汽車產量一定高于第三季度的汽車產量”,你覺得圓圓說的對嗎?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,已知△ABC和△BDE都是等邊三角形.則下列結論:①AE=CD;②BF=BG;③∠AHC=60°;④△BFG是等邊三角形;⑤HB平分∠AHD.其中正確的有( )

A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com