
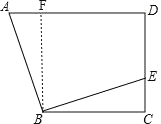
【題目】如圖,在四邊形ABCD中,AD∥BC,∠C=90°,BC=CD=8,過點B作EB⊥AB,交CD于點E.若DE=6,則AD的長為( )

A.6 B.8 C.9 D.10
【答案】D
【解析】
試題分析:首先作BF⊥AD與點F,推得BF∥CD,判斷出四邊形BCDF是矩形;然后根據BC=CD=8,可得四邊形BCDF是正方形,所以BF=BC;最后根據全等三角形的判定方法,證明△BCE≌△BAF,即可推得AF=CE,進而求出AD的長為多少即可.
如圖,作BF⊥AD與點F,
 ,
,
∵BF⊥AD, ∴∠AFB=BFD=90°, ∵AD∥BC, ∴∠FBC=∠AFB=90°, ∵∠C=90°,
∴∠C=∠AFB=∠BFD=∠FBC=90°. ∴四邊形BCDF是矩形. ∵BC=CD,∴四邊形BCDF是正方形, ∴BC=BF=FD. ∵EB⊥AB, ∴∠ABE=90°, ∴∠ABE=∠FBC, ∴∠ABE﹣∠FBE=∠FBC﹣∠FBE, ∴∠CBE=∠FBA. 在△BAF和△BEC中, 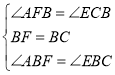 , ∴△BAF≌△BEC, ∴AF=EC. ∵CD=BC=8,DE=6, ∴DF=8,EC=2, ∴AF=2, ∴AD=8+2=10.
, ∴△BAF≌△BEC, ∴AF=EC. ∵CD=BC=8,DE=6, ∴DF=8,EC=2, ∴AF=2, ∴AD=8+2=10.


科目:初中數學 來源: 題型:
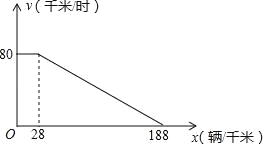
【題目】“城市發展 交通先行”,成都市今年在中心城區啟動了緩堵保暢的二環路高架橋快速通道建設工程,建成后將大大提升二環路的通行能力.研究表明,某種情況下,高架橋上的車流速度V(單位:千米/時)是車流密度x(單位:輛/千米)的函數,且當0<x≤28時,V=80;當28<x≤188時,V是x的一次函數.函數關系如圖所示.
(1)求當28<x≤188時,V關于x的函數表達式;
(2)若車流速度V不低于50千米/時,求當車流密度x為多少時,車流量P(單位:輛/時)達到最大,并求出這一最大值.
(注:車流量是單位時間內通過觀測點的車輛數,計算公式為:車流量=車流速度×車流密度)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列幾種說法中,不正確的有_____(只填序號)
①幾個有理數相乘,若負因數為奇數個,則積為負數,
②如果兩個數互為相反數,則它們的商為﹣1,
③一個數的絕對值一定不小于這個數,
④﹣a的絕對值等于a.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我國首艘國產航母于 2018 年 4 月 26 日正式下水,排水量約為 65000 噸,將65000 用科學記數法表示為( )
A. 6.5×10-4 B. 6.5 ×104 C. ﹣6.5×104 D. 0.65×104
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】.2015年5月6日涼山州政府在邛海“空列”項目考察座談會上與多方達成初步合作意向,決定共同出資60.8億元,建設40千米的環邛海空中列車,這將是國內第一條空中列車,據測算,將有24千米的“空列”軌道架設在水上,其余架設在陸地上,并且每千米水上建設費用比陸地建設費用多0.2億元.
(1)求每千米“空列”軌道的水上建設費用和陸地建設費用各需多少億元.
(2)預計在某段“空列”軌道的建設中,每天至少需要運送沙石1600 m3,施工方準備租用大、小兩種運輸車共10輛,已知每輛大車每天運送沙石200 m3,每輛小車每天運送沙石120 m3,大、小車每天每輛租車費用分別為1000元、700元,且要求每天租車的總費用不超過9300元,則施工方有幾種租車方案?哪種租車方案費用最低?最低費用是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com