【題目】如圖，EF是Rt△ABC的中位線，∠BAC＝90°，AD是斜邊BC邊上的中線，EF和AD相交于點O，則下列結論不正確的是（ ）
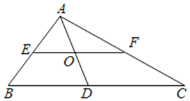
A. AO＝ODB. EF＝ADC. S△AEO＝S△AOFD. S△ABC＝2S△AEF
【答案】D
【解析】
根據三角形中位線定理以及直角三角形斜邊上的中線等于斜邊的一半逐項分析即可．
解：
∵EF是Rt△ABC的中位線，
∴EF
BC ,
∵AD是斜邊BC邊上的中線，
∴AD=BC，
∴EF=AD，故選項B正確；
∵AE=BE，EO∥BD，
∴AO=OD，故選項A正確；
∵E，O，F，分別是AB，AD，AC中點，
∴EO=BD，OF=DC，
∵BD=CD，
∴OE=OF，
又∵EF∥BC，
∴S△AEO=S△AOF，故選項C正確；
∵EF∥BC，
∴△ABC∽△AEF，
∵EF是Rt△ABC的中位線，
∴S△ABC：S△AEF=4：1，
即S△ABC=4S△AEF≠2S△AEF，故選D錯誤，
故選：D．
怎樣學好牛津英語系列答案科目：初中數學 來源： 題型：
【題目】在
中，
于點
（1）如圖1，若
的角平分線交
于點
，
，
，求
的度數；
（2）如圖2，點
分別在線段
上，將折疊，點
落在點
處，點
落在點
處，折痕分別為
和
，且點，點均在直線
上，若
，試猜想
與
之間的數量關系，并加以證明；
（3）在（2）小題的條件下，將
繞點逆時針旋轉一個角度
（
），記旋轉中的為
（如圖3），在旋轉過程中，直線
與直線
交于點
，直線與直線交于點
，若
，是否存在這樣的
兩點，使
為直角三角形？若存在，請直接寫出旋轉角的度數；若不存在，請說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】
開通了，中國聯通公布了資費標準，其中包月
元時，超出部分國內撥打
元/分．由于業務多，小明的爸爸打電話已超出了包月費．下表是超出部分國內撥打的收費標準．
時間/分 | 1 | 2 | 3 | 4 | 5 | … |
電話費/元 | 0.36 | 0.72 | 1.08 | 1.44 | 1.80 | … |
（1）這個表反映了哪兩個變量之間的關系？哪個是自變量？哪個是因變量？
（2）如果用
表示超出時間，
表示超出部分的電話費，那么與的關系式是什么？
（3）如果打電話超出
分鐘，需多付多少電話費？
（4）某次打電話的費用超出部分是
元，那么小明的爸爸打電話超出幾分鐘？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，將△ABC繞點A逆時針旋轉80°后得到△A′B′C′（點B的對應點是點B′，點C的對應點是點C′，連接BB′，若∠B′BC=20°，則∠BB′C′的大小是（ ）
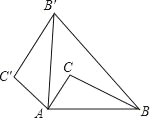
A. 82° B. 80° C. 78° D. 76°
查看答案和解析>>
科目：初中數學 來源： 題型：
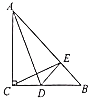
【題目】如圖，在
中，
，
，
是
的平分線，折疊
使得點
落在
邊上的
處，連接
、
.下列結論：①
；②
是等腰三角形；③
；④
.其中正確的結論是______．（填寫序號）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在
中，
，
是中線，作關于
的軸對稱圖形
.
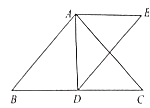
（1）直接寫出和
的位置關系；
（2）連接
，寫出
和的數量關系，并說明理由；
（3）當
，
時，在上找一點
，使得點到點
與到點
的距離之和最下小，求
的面積.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在矩形ABCD中，點E為CD上一點，將△BCE沿BE翻折后點C恰好落在AD邊上的點F處，過F作FH⊥BC于H，交BE于G，連接CG．
（1）求證：四邊形CEFG是菱形；
（2）若AB=8，BC=10，求四邊形CEFG的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，直線y＝k1x＋b與雙曲線y＝
相交于A(1,2)、B(m，－1)兩點．
(1)求直線和雙曲線的解析式；
(2)若A1(x1，y1)、A2(x2，y2)、A3(x3，y3)為雙曲線上的三點，且x1＜x2＜0＜x3，請直接寫出y1、y2、y3的大小關系式；
(3)觀察圖象，請直接寫出不等式k1x＋b＞的解集．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
