
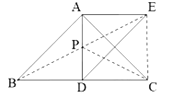
【題目】如圖,在![]() 中,
中,![]() ,
,![]() 是中線,作
是中線,作![]() 關于
關于![]() 的軸對稱圖形
的軸對稱圖形![]() .
.
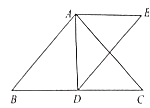
(1)直接寫出![]() 和
和![]() 的位置關系;
的位置關系;
(2)連接![]() ,寫出
,寫出![]() 和
和![]() 的數量關系,并說明理由;
的數量關系,并說明理由;
(3)當![]() ,
,![]() 時,在
時,在![]() 上找一點
上找一點![]() ,使得點
,使得點![]() 到點
到點![]() 與到點
與到點![]() 的距離之和最下小,求
的距離之和最下小,求![]() 的面積.
的面積.
【答案】(1)垂直;(2)![]() .理由見解析;(3)
.理由見解析;(3)![]() .
.
【解析】
(1)根據對稱點連線垂直于對稱軸,即可確定AC⊥DE;(2)連接CE,證明四邊形AECD是正方形,在結合三角形ABC是等腰三角形,即可說明;(3)先證明.△ACD≌△ABD,得到點B和點C關于AD成軸對稱;連接![]() ,交
,交![]() 于點
于點![]() ,且當
,且當![]() ,
,![]() ,
,![]() 三點在同一條直線上,點
三點在同一條直線上,點![]() 到點
到點![]() 與到點
與到點![]() 的距離之和最小,然后結合(1)的結論,運用三角形的面積公式即可求得.
的距離之和最小,然后結合(1)的結論,運用三角形的面積公式即可求得.
解:(1)垂直
(2)![]() .理由如下:
.理由如下:
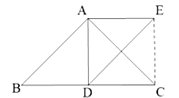
![]() 關于
關于![]() 的軸對稱圖形為
的軸對稱圖形為![]() .
.
![]() ,
,![]()
在![]() 和
和![]() 中,
中,
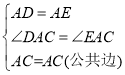
![]()
![]()
又![]() 是邊
是邊![]() 上的中線
上的中線
![]() .
.
![]() .
.
(3)在![]() 和
和![]() 中
中
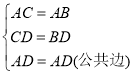
![]()
![]()
![]()
![]()
![]() 點
點![]() 和點
和點![]() 關于
關于![]() 成軸對稱
成軸對稱
連接![]() ,交
,交![]() 于點
于點![]() ,如圖所示
,如圖所示
![]()
![]()
且當![]() ,
,![]() ,
,![]() 三點在同一條直線上,點
三點在同一條直線上,點![]() 到點
到點![]() 與到點
與到點![]() 的距離之和最小
的距離之和最小
![]()
![]()
在![]() 中,.
中,.![]()
由(1)知,![]() ,
,
![]()
![]()
![]()
![]()
![]()


科目:初中數學 來源: 題型:
【題目】某校組織1000名學生參加“展示我美麗祖國”慶國慶的自拍照片的評比活動.隨機機取一些學生在評比中的成績制成的統計圖表如下:


根據以上圖表提供的信息,解答下列問題:
(1)寫出表中a、b的數值:a ,b ;
(2)補全頻數分布表和頻數分布直方圖;
(3)如果評比成績在95分以上(含95 分)的可以獲得一等獎,試估計該校參加此次活動獲得一等 獎的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學對全校學生進行文明禮儀知識測試,為了解測試結果,隨機抽取部分學生的成績進行分析,將成績分為三個等級:不合格、一般、優秀,并繪制成如下兩幅統計圖(不完整).
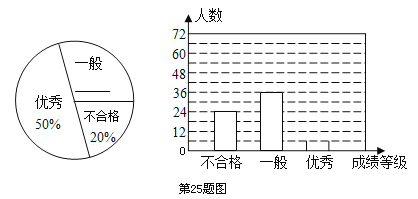
請你根據圖中所給的信息解答下列問題:
(1)請將以上兩幅統計圖補充完整;
(2)若“一般”和“優秀”均被視為達標成績,則該校被抽取的學生中有______人達標;
(3)若該校學生有1000人,請你估計此次測試中,全校達標的學生有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,EF是Rt△ABC的中位線,∠BAC=90°,AD是斜邊BC邊上的中線,EF和AD相交于點O,則下列結論不正確的是( )
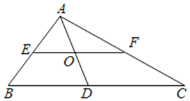
A. AO=ODB. EF=ADC. S△AEO=S△AOFD. S△ABC=2S△AEF
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對一張矩形紙片ABCD進行折疊,具體操作如下:
第一步:先對折,使AD與BC重合,得到折痕MN,展開;
第二步:再一次折疊,使點A落在MN上的點A′處,并使折痕經過點B,得到折痕BE,同時,得到線段BA′,EA′,展開,如圖1;
第三步:再沿EA′所在的直線折疊,點B落在AD上的點B′處,得到折痕EF,同時得到線段B′F,展開,如圖2.
求證:(1)∠ABE=30°;
(2)四邊形BFB′E為菱形.
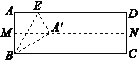

圖1 圖2
查看答案和解析>>
科目:初中數學 來源: 題型:
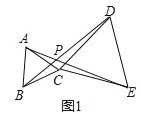
【題目】△ABC和△CDE是以C為公共頂點的兩個三角形.
(1)如圖1,當△ABC和△CDE都是等邊三角形時,連接BD、AE相交于點P.求∠DPE的度數;
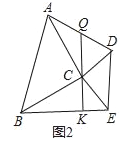
(2)如圖2,當△ABC和△CDE都是等腰直角三角形,且∠ACB=∠DCE=90°時,連接AD、BE,Q為AD中點,連接QC并延長交BE于K.求證:QK⊥BE;
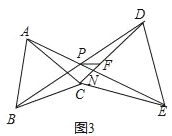
(3)在(1)的條件下,N是線段AE與CD的交點,PF是∠DPE的平分線,與DC交于點F,CN=2![]() ,∠PFN=45°,求FN的長.
,∠PFN=45°,求FN的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
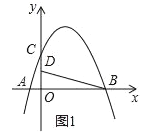
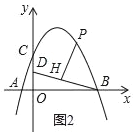
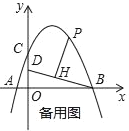
【題目】如圖,在平面直角坐標系中,拋物線y=ax2+bx+4交x軸于點A(﹣2,0)和B(B在A右側),交y軸于點C,直線y=![]() 經過點B,交y軸于點D,且D為OC中點.
經過點B,交y軸于點D,且D為OC中點.
(1)求拋物線的解析式;
(2)若P是第一象限拋物線上的一點,過P點作PH⊥BD于H,設P點的橫坐標是t,線段PH的長度是d,求d與t的函數關系式;
(3)在(2)的條件下,當d=![]() 時,將射線PH繞著點P順時針方向旋轉45°交拋物線于點Q,求點Q的坐標.
時,將射線PH繞著點P順時針方向旋轉45°交拋物線于點Q,求點Q的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)①如圖1,已知![]() ,
,![]() ,可得
,可得![]() __________.
__________.

②如圖2,在①的條件下,如果![]() 平分
平分![]() ,則
,則![]() __________.
__________.

③如圖3,在①、②的條件下,如果![]() ,則
,則![]() __________.
__________.

(2)嘗試解決下面問題:已知如圖4,![]() ,
,![]() ,
,![]() 是
是![]() 的平分線,
的平分線,![]() ,求
,求![]() 的度數.
的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,動點P在射線CB上(與B、C不重合),連結AP,過D作DF∥AP交直線BC于點F,過F作FE⊥直線BD于點E,連結AE、PE.
(1)如圖,當點P在線段CB上時
①求證:△ABP≌△DCF;
②點P在運動過程中,探究:△AEP的形狀是否發生變化,若不變,請判斷△AEP的形狀,并說明理由;
(2)如圖,當點P在CB的延長線上時,若正方形ABCD的邊長為1,設BP=x,當x為何值時,DF平分∠BDC?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com