
【題目】如圖,在平面直角坐標系中,四邊形ABCD為正方形,已知點A(﹣6,0),D(﹣7,3),點B、C在第二象限內.
(1)求點B的坐標。
(2)將正方形ABCD以每秒1個單位的速度沿x軸向右平移t秒,若存在某一時刻t,使在第一象限內點B、D兩點的對應點B′、D′正好落在某反比例函數的圖象上,請求出此時t的值以及這個反比例函數的解析式;
(3)在(2)的情況下,問是否存在x軸上的點P和反比例函數圖象上的點Q,使得以P、Q、B′、D′四個點為頂點的四邊形是平行四邊形?若存在,請直接寫出符合題意的點P、Q的坐標;若不存在,請說明理由.

【答案】(1)B(﹣3,1);
(2)t的值為9,反比例函數解析式為y=![]() ;
;
(3)符合題意的點P、Q的坐標為P(![]() ,0)、Q(
,0)、Q(![]() ,4)或P(7,0)、Q(3,2).
,4)或P(7,0)、Q(3,2).
【解析】(1)過程略B(﹣3,1)
解:(2)設反比例函數為y=![]() ,
,
由題意得:點B′坐標為(﹣3+t,1),點D′坐標為(﹣7+t,3),
∵點B′和D′在該比例函數圖象上,
∴k=(﹣3+t)×1=(﹣7+t)×3,[來源:]
解得:t=9,k=6,
∴反比例函數解析式為y=![]() .
.
(3) )假設存在,設點P的坐標為(m,0),點Q的坐標為(n,![]() ).
).
以P、Q、B′、D′四個點為頂點的四邊形是平行四邊形分兩種情況:
①當B′D′為對角線時,設線段B′D′的中點為M,如圖2所示.

∵點B′(6,1),點D′(2,3),點M為線段B′D′的中點,
∴點M的坐標為(4,2),
∵點M是線段PQ的中點,
∴ ,解得:
,解得:![]() ,
,
∴P(![]() ,0),Q(
,0),Q(![]() ,4);
,4);
②當B′D′為邊時.
∵四邊形PQB′D′為平行四邊形,
∴ ,解得:
,解得:![]() ,
,
∴P(7,0),Q(3,2).
綜上可知:存在x軸上的點P和反比例函數圖象上的點Q,使得以P、Q、B′、D′四個點為頂點的四邊形是平行四邊形,符合題意的點P、Q的坐標為P(![]() ,0)、Q(
,0)、Q(![]() ,4)或P(7,0)、Q(3,2).
,4)或P(7,0)、Q(3,2).


科目:初中數學 來源: 題型:
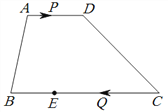
【題目】如圖,在梯形ABCD中,AD∥BC,AD=8,BC=15,點E在BC邊上,且CE=2BE。點P以每秒1個單位長度的速度從點A出發,沿AD向點D運動;點Q同時以每秒3個單位長度的速度從點C出發,沿CB向點B運動,當其中一個點停止運動時,另一個點也隨之停止運動。當運動時間t=______秒時,以點P,Q,E,D為頂點的四邊形是平行四邊形。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某電腦公司銷售部為了定制下個月的銷售計劃,對20位銷售員本月的銷售量進行了統計,繪制成如圖所示的統計圖,則這20位銷售人員本月銷售量的平均數、中位數、眾數分別是( )
A.19,20,14
B.19,20,20
C.18.4,20,20
D.18.4,25,20
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(10分)如圖,在矩形ABCD中,E,F為BC上兩點,且BE=CF,連接AF,DE交于點O.
求證:(1)△ABF≌△DCE;
(2)△AOD是等腰三角形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=x2+bx+c(b,c為常數).
(1)當b=2,c=﹣3時,求二次函數圖象的頂點坐標;
(2)當c=10時,若在函數值y=1的情況下,只有一個自變量x的值與其對應,求此時二次函數的解析式;
(3)當c=b2時,若在自變量x的值滿足b≤x≤b+3的情況下,與其對應的函數值y的最小值為21,求此時二次函數的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列關于函數 ![]() 的四個命題:①當
的四個命題:①當 ![]() 時,
時, ![]() 有最小值10;②
有最小值10;② ![]() 為任意實數,
為任意實數, ![]() 時的函數值大于
時的函數值大于 ![]() 時的函數值;③若
時的函數值;③若 ![]() ,且
,且 ![]() 是整數,當
是整數,當 ![]() 時,
時, ![]() 的整數值有
的整數值有 ![]() 個;④若函數圖象過點
個;④若函數圖象過點 ![]() 和
和 ![]() ,其中
,其中 ![]() ,
, ![]() ,則
,則 ![]() .其中真命題的序號是( )
.其中真命題的序號是( )
A.①
B.②
C.③
D.④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)方法回顧:在學習三角形中位線時,為了探索三角形中位線的性質,思路如下:
第一步添加輔助線:如圖1,在![]() 中,延長
中,延長![]() (
(![]() 分別是
分別是![]() 的中點)到點
的中點)到點![]() ,使得
,使得![]() ,連接
,連接![]() ;
;
第二步證明![]() ,再證四邊形
,再證四邊形![]() 是平行四邊形,從而得出三角形中位線的性質結論:____________________________________(請用DE與BC表示)
是平行四邊形,從而得出三角形中位線的性質結論:____________________________________(請用DE與BC表示)
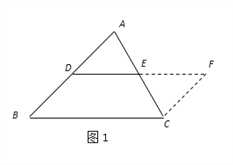
(2)問題解決:如圖2,在正方形ABCD中,E為AD的中點,G、F分別為AB、CD邊上的點,若AG=2,DF=3,∠GEF=90°,求GF的長.

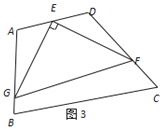
(3)拓展研究:如圖3,在四邊形ABCD中,∠A=105°,∠D=120°,E為AD的中點,G、F分別為AB、CD邊上的點,若AG=![]() ,DF=2,∠GEF=90°,求GF的長.
,DF=2,∠GEF=90°,求GF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校在“數學小論文”評比活動中,共征集到論文100篇,對論文評比的分數(分數為整數)整理后,分組畫出頻數分布直方圖(如圖),已知從左到右5個小長方形的高的比為l:3:7:6:3,那么在這次評比中被評為優秀的論文(分數大于或等于80分為優秀)有____篇.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com