
【題目】下面說法正確的是( ).
A. 檢測一批進口食品的質量應采用全面調查
B. 從![]() 萬名考生的成績中抽取
萬名考生的成績中抽取![]() 名考生的成績作為樣本,樣本容量是
名考生的成績作為樣本,樣本容量是![]() 萬
萬
C. 反應你本學年數學成績的變化情況宜采用扇形統計圖
D. 一組數據的樣本容量是![]() ,最大值是
,最大值是![]() ,最小值是
,最小值是![]() ,取組距為
,取組距為![]() ,可分為
,可分為![]() 組
組
 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】我們知道平行四邊形有很多性質,現在如果我們把平行四邊形沿著它的一條對角線翻折,會發現這其中還有更多的結論.
(發現與證明)![]() 中,
中,![]() ,將
,將![]() 沿
沿![]() 翻折至
翻折至![]() ,連結
,連結![]() .
.
結論1:![]() 與
與![]() 重疊部分的圖形是等腰三角形;
重疊部分的圖形是等腰三角形;
結論2:![]() .
.
試證明以上結論.
(應用與探究)
在![]() 中,已知
中,已知![]() ,
,![]() ,將
,將![]() 沿
沿![]() 翻折至
翻折至![]() ,連結
,連結![]() .若以
.若以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形是正方形,求
為頂點的四邊形是正方形,求![]() 的長.(要求畫出圖形)
的長.(要求畫出圖形)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明為了測量樓房AB的高度,他從樓底的B處沿著斜坡向上行走20m,到達坡頂D處.已知斜坡的坡角為15°.(以下計算結果精確到0.1m)
(1)求小明此時與地面的垂直距離CD的值;
(2)小明的身高ED是1.6m,他站在坡頂看樓頂A處的仰角為45°,求樓房AB的高度.(sin15°≈0.2588,cos15°≈0.9659 ,tan≈.0.2677 )

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學活動課上,同學們探究了角平分線的作法.下面給出三個同學的作法:
小紅的作法
如圖,∠AOB是一個任意角,在邊OA、OB上分別取OM=ON,再過點O作MN的垂線,垂足為P,則射線OP便是∠AOB的平分線.

小明的作法 如圖,∠AOB是一個任意角,在邊OA、OB上分別取OM=ON,移動角尺,使角尺兩邊相同的刻度分別與M,N重合,過角尺頂點C的射線OC便是∠AOB的平分線.
|
小剛的作法 如圖,∠AOB是一個任意角,在邊OA、OB上分別取OM=ON,再分別過點M,N作OA,OB的垂線,交點為P,則射線OP便是∠AOB的平分線.
|
請根據以上情境,解決下列問題
(1)小紅的作法依據是 .
(2)為說明小明作法是正確的,請幫助他完成證明過程.
證明:∵OM=ON,OC=OC, ,
∴△OMC≌△ONC( )(填推理的依據)
(3)小剛的作法正確嗎?請說明理由
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數![]() 的圖像與反比例函數
的圖像與反比例函數![]() 的圖像相交于
的圖像相交于![]() 、
、![]() 兩點.
兩點.

(1)求出兩函數解析式;
(2)根據圖像回答:當![]() 為何值時,一次函數的函數值大于反比例函數的函數值?
為何值時,一次函數的函數值大于反比例函數的函數值?
(3)連接![]() 、
、![]() ,試求
,試求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 在平面直角坐標系
在平面直角坐標系![]() 中,
中,
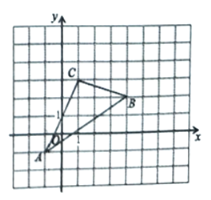
(1)請直接寫出![]() 、
、![]() 兩點的坐標;
兩點的坐標;
(2)若把![]() 向上平移
向上平移![]() 個單位,再向右平移
個單位,再向右平移![]() 個單位得
個單位得![]() ,請在圖中畫出
,請在圖中畫出![]() ,并寫出點
,并寫出點![]() 的坐標;
的坐標;
(3)求![]() 的面積。
的面積。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,正方形ABCD的位置如右圖所示,點A的坐標為(1,0),點D的坐標為(0,2).延長CB交x軸于點A1,作正方形A1B1C1C;延長C1B1交x軸于點A2,作正方形A2B2C2C1,…按這樣的規律進行下去,第2017個正方形的面積為_____.
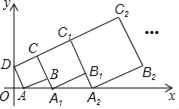
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,頂點M在y軸上的拋物線與直線y=x+1相交于A、B兩點,且點A在x軸上,點B的橫坐標為2,連結AM、BM.
(1)求拋物線的函數關系式;
(2)判斷△ABM的形狀,并說明理由;
(3)把拋物線與直線y=x的交點稱為拋物線的不動點.若將(1)中拋物線平移,使其頂點為(m,2m),當m滿足什么條件時,平移后的拋物線總有不動點.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,拋物線C:y=x2經過變化可得到拋物線C1:y1=a1x(x﹣b1),C1與x軸的正半軸交與點A1,且其對稱軸分別交拋物線C,C1于點B1,D1,此時四邊形OB1A1D1恰為正方形;按上述類似方法,如圖2,拋物線C1:y1=a1x(x﹣b1)經過變換可得到拋物線C2:y2=a2x(x﹣b2),C2與x軸的正半軸交與點A2,且其對稱軸分別交拋物線C1,C2于點B2,D2,此時四邊形OB2A2D2也恰為正方形;按上述類似方法,如圖3,可得到拋物線C3:y3=a3x(x﹣b3)與正方形OB3A3D3.請探究以下問題:
(1)填空:a1= ,b1= ;
(2)求出C2與C3的解析式;
(3)按上述類似方法,可得到拋物線Cn:yn=anx(x﹣bn)與正方形OBnAnDn(n≥1).
①請用含n的代數式直接表示出Cn的解析式;
②當x取任意不為0的實數時,試比較y2015與y2016的函數值的大小并說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com