【答案】
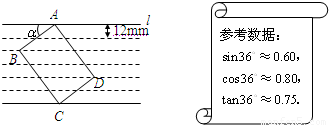
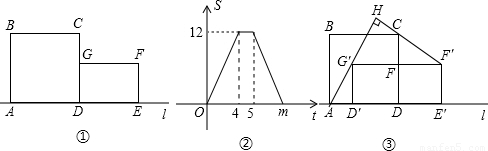
分析:(1)由圖②的函數圖象知:從第4-5秒,S的值恒為12,即此時矩形全部落在正方形的內部,由此可求得兩個條件:①矩形的面積為12,②正方形的邊長為1+DE,根據這兩個條件求解即可.
(2)當0≤t≤5時,矩形在直線AB的左側,可用t表示出AD′、PF′的長,易求得D′G、CP的長,即可用勾股定理求得AG′
2、CF′
2的值,即可得到y、t的函數關系式.
(3)此題要分五種情況討論:
①當0≤t<4時,點E′在D點右側;由于∠HG′F′、∠HF′G′都是銳角,顯然直線AG′與CF′不可能平行;當兩條直線垂直時,△G′HF′是直角三角形,易證得△AD′G′∽△CPF′,根據相似三角形得到的比例線段即可求得t的值;
②當t=4時,D、E′重合,此時直線DC與E′F′重合,顯然此時AG′與CF′既不平行也不垂直,因為過直線外一點,有且只有一條直線與已知直線平行或垂直;
③當4<t<5時,矩形在正方形的內部,延長G′F′交BC于P,延長AG′交CD于Q,此時∠CF′P是銳角,所以∠CF′G是鈍角,顯然AG′與CF′不可能垂直;當兩直線平行時,可證得△AD′G′∽△F′PC,進而可根據相似三角形得到的比例線段求得t的值;
④當t=5時,此種情況與②相同;
⑤當5<t<9時,此時∠QG′F′與∠CF′G′都是鈍角,顯然AG′與CF′不可能平行;當兩直線垂直時,可延長CF′與AG′相交于點M,延長G′F′與CD相交于點P,通過證△AD′G′∽△CPF′來求得此時t的值.
解答:解:(1)由圖②知:從第4到第5秒時,S的值恒為12,此時矩形全部落在正方形的內部,
那么矩形的面積為12,即可求得DE=4;
這個過程持續了1秒,說明正方形的邊長為:DE+1=5;
由于矩形的速度恒定,所以5~m也應該用4秒的時間,故m=5+4=9;
即:b=4,a=5,m=9.
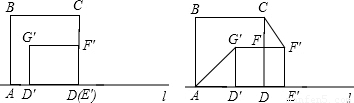
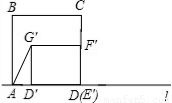
(2)如圖,當0≤t≤5時,
∵AD′=5-t,D′G=3,PF′=4-t,CP=2,
∴y=9+(5-t)
2+4+(4-t)
2,
∴y=2(t-

)
2+
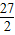
,
∴當t=

時,y有最小值,y
最小值=
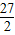
.
(3)①當0≤t<4時,分別延長AG′和F′C;
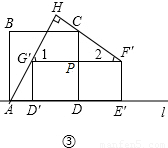
如圖,由于∠1和∠2都是銳角,所以∠1+∠2<180°,
所以AG′與CF′不可能平行.
設AG′與F′C的延長線交于點H,
當∠G′AD′=∠PCF′時,直線AG′⊥CF′;
∴△AD′G′∽△CPF′,
∴
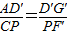
,
∴
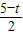
=
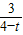
,
解得t
1=2,t
2=7(不合題意,舍去).
②當t=4時,由于點F′在CD上,而點G′不在直線AD上,
因為AD⊥CD,所以AG′不可能也垂直于CD
(因為過直線外一點有且只有一條直線與已知直線垂直).
同樣,由于AB∥CD,而點G′不在直線AB上,
所以t=4時,AG′也不可能平行于CD(CF′)
(因為過直線外一點,有且只有一條直線與已知直線平行).
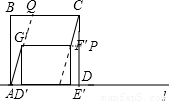
③4<t<5時,延長G′F′交PC于P,延長AG′交CD于Q,
由于∠CF′P是銳角,所以∠CF′G是鈍角,
所以∠CF′G+∠QGF′≠90°,所以AG′與CF′不可能垂直;
當∠G′AD′=∠CF′P時,AG′∥CF′,
易得△AD′G′∽△F′PC,
∴
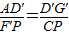
,
∴
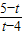
=

,
解得t=4.4.
④當t=5時,AG′與CF′既不可能垂直也不可能平行,理由同②.
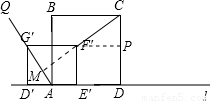
⑤當5<t<9時,因為∠QG′F′與∠CF′G′都是鈍角,
所以∠QG′F′+∠CF′G′>180°,
所以AG′與CF′不可能平行.
延長CF′與AG′相交于點M,延長G′F′與CD相交于點P;
當∠MG′F′+∠MF′G′=90°時,AG′⊥CF′;
又∵∠AG′D′+∠AG′F′=90°,∠MF′G′=∠CF′P,
∴∠AG′D′=∠CF′P,又∠AD′G′=∠F′PC,
∴△AD′G′∽△CPF′,
∴
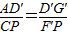
,即
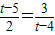
;
解得:t
1=2(不合題意,舍去),t
2=7;
所以,綜上所述,當t=2或t=7時,直線AG′與直線CF′垂直,當t=4.4時,直線AG′與直線CF′平行.
點評:此題主要考查了矩形、正方形的性質,勾股定理,相似三角形的判定和性質以及分段函數的應用等知識,同時還考查了分類討論的數學思想,難度較大.

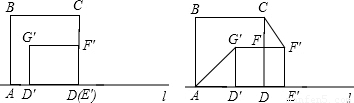
 )2+
)2+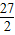 ,
, 時,y有最小值,y最小值=
時,y有最小值,y最小值=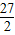 .
.
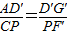 ,
,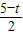 =
=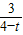 ,
, ②當t=4時,由于點F′在CD上,而點G′不在直線AD上,
②當t=4時,由于點F′在CD上,而點G′不在直線AD上, ③4<t<5時,延長G′F′交PC于P,延長AG′交CD于Q,
③4<t<5時,延長G′F′交PC于P,延長AG′交CD于Q,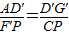 ,
,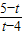 =
= ,
, ⑤當5<t<9時,因為∠QG′F′與∠CF′G′都是鈍角,
⑤當5<t<9時,因為∠QG′F′與∠CF′G′都是鈍角,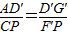 ,即
,即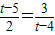 ;
;