
【題目】鄭州市精準(zhǔn)扶貧工作已進(jìn)入攻堅(jiān)階段.貧困戶張伯伯在相關(guān)單位的幫扶下把一片坡地改造后種植了優(yōu)質(zhì)水果藍(lán)莓,今年正式上市銷售在銷售的30天中,第一天賣出20千克為了擴(kuò)大銷量采取了降價(jià)措施以后每天比前一天多賣出4千克第![]() 天的售價(jià)為
天的售價(jià)為![]() 元/千克,
元/千克,![]() 關(guān)于
關(guān)于![]() 的函數(shù)解析式為
的函數(shù)解析式為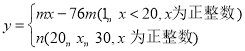 ,且第12天的售價(jià)為32元/千克,第26天的售價(jià)為25元/千克.已知種植銷售藍(lán)莓的成本是18元/千克,每天的利潤是
,且第12天的售價(jià)為32元/千克,第26天的售價(jià)為25元/千克.已知種植銷售藍(lán)莓的成本是18元/千克,每天的利潤是![]() 元(利潤=銷售收入
元(利潤=銷售收入![]() 成本).
成本).
(1)![]() _____________,
_____________,![]() ____________;
____________;
(2)求銷售藍(lán)莓第幾天時(shí),當(dāng)天的利潤最大?最大利潤是多少?
(3)在銷售藍(lán)莓的30天中,當(dāng)天利潤不低于870元的共有多少天?
【答案】(1)![]() ,
,![]() ;(2)當(dāng)
;(2)當(dāng)![]() 時(shí),
時(shí),![]() 最大
最大![]() ;(3)當(dāng)天利潤不低于870元的天數(shù)共有12天
;(3)當(dāng)天利潤不低于870元的天數(shù)共有12天
【解析】
(1)根據(jù)題意將相關(guān)數(shù)值代入即可;
(2)在(1)的基礎(chǔ)上分段表示利潤,討論最值;
(3)分別在(2)中的兩個(gè)函數(shù)取值范圍內(nèi)討論利潤不低于870的天數(shù),注意天數(shù)為正整數(shù).
解:(1)當(dāng)?shù)?/span>12天的售價(jià)為32元/件,代入y=mx-76m得
32=12m-76m
解得m=-![]()
當(dāng)?shù)?/span>26天的售價(jià)為25元/千克時(shí),代入y=n
則n=25
故答案為:m=-![]() ,n=25
,n=25
(2)由(1)第![]() 大的銷件量為
大的銷件量為![]()
當(dāng)![]() 時(shí),
時(shí),![]()
![]()
![]()
∴當(dāng)![]() 時(shí),
時(shí),![]() 最大
最大![]()
當(dāng)![]() 時(shí),
時(shí),![]() ,
,
![]() ,
,![]() 隨
隨![]() 的增大而增大,
的增大而增大,
∴當(dāng)![]() 時(shí),
時(shí),![]() 最大
最大![]()
![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí),![]() 最大
最大![]() .
.
(3)當(dāng)![]() 時(shí),令
時(shí),令![]() ,
,
解得![]() .
.
∵拋物線![]() 的開口向下,
的開口向下,
![]() 時(shí),
時(shí),![]() ,
,![]()
![]() 為正整數(shù),
為正整數(shù),
![]() 有9天利潤不低于870元.
有9天利潤不低于870元.
當(dāng)![]() 時(shí),令
時(shí),令![]() ,解得
,解得![]() ,
,
![]() ,
,
![]() 為正整數(shù),
為正整數(shù),![]() 有3天利潤不低于870元.
有3天利潤不低于870元.
![]() 綜上所述,當(dāng)天利潤不低于870元的天數(shù)共有12天.
綜上所述,當(dāng)天利潤不低于870元的天數(shù)共有12天.


 名校課堂系列答案
名校課堂系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】對于實(shí)數(shù)![]() ,若存在坐標(biāo)
,若存在坐標(biāo)![]() 同時(shí)滿足一次函數(shù)
同時(shí)滿足一次函數(shù)![]() 和反比例函數(shù)
和反比例函數(shù)![]() ,則二次函數(shù)
,則二次函數(shù)![]() 為一次函數(shù)和反比例函數(shù)的“共享”函數(shù).
為一次函數(shù)和反比例函數(shù)的“共享”函數(shù).
(1)試判斷(需要寫出判斷過程):一次函數(shù)![]() 和反比例函數(shù)
和反比例函數(shù)![]() 是否存在“共享”函數(shù)?若存在,寫出它們的“共享”函數(shù)和實(shí)數(shù)對坐標(biāo);
是否存在“共享”函數(shù)?若存在,寫出它們的“共享”函數(shù)和實(shí)數(shù)對坐標(biāo);
(2)已知整數(shù)![]() 滿足條件:
滿足條件:![]() ,并且一次函數(shù)
,并且一次函數(shù)![]() 與反比例函數(shù)
與反比例函數(shù)![]() 存在“共享”函數(shù)
存在“共享”函數(shù)![]() ,求整數(shù)
,求整數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某社區(qū)組織了以“奔向幸福,‘毽’步如飛”為主題的踢毽子比賽活動(dòng),初賽結(jié)束后有甲、乙兩個(gè)代表隊(duì)進(jìn)入決賽,已知每隊(duì)有5名隊(duì)員,按團(tuán)體總數(shù)排列名次,在規(guī)定時(shí)間內(nèi)每人踢100個(gè)以上(含100)為優(yōu)秀.下表是兩隊(duì)各隊(duì)員的比賽成績.
1 號 | 2 號 | 3 號 | 4 號 | 5 號 | 總數(shù) | |
甲隊(duì) | 103 | 102 | 98 | 100 | 97 | 500 |
乙隊(duì) | 97 | 99 | 100 | 96 | 108 | 500 |
經(jīng)統(tǒng)計(jì)發(fā)現(xiàn)兩隊(duì)5名隊(duì)員踢毽子的總個(gè)數(shù)相等,按照比賽規(guī)則,兩隊(duì)獲得并列第一.學(xué)習(xí)統(tǒng)計(jì)知識(shí)后,我們可以通過考查數(shù)據(jù)中的其它信息作為參考,進(jìn)行綜合評定:
(1)甲、乙兩隊(duì)的優(yōu)秀率分別為 ;
(2)甲隊(duì)比賽數(shù)據(jù)的中位數(shù)為 個(gè);乙隊(duì)比賽數(shù)據(jù)的中位數(shù)為 個(gè);
(3)分別計(jì)算甲、乙兩隊(duì)比賽數(shù)據(jù)的方差;
(4)根據(jù)以上信息,你認(rèn)為綜合評定哪一個(gè)隊(duì)的成績好?簡述理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
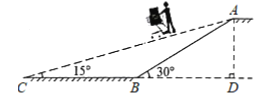
【題目】某市商場為方便消費(fèi)者購物,準(zhǔn)備將原來的階梯式自動(dòng)扶梯改造成斜坡式自動(dòng)扶梯.如圖所示,已知原階梯式自動(dòng)扶梯![]() 長為
長為![]() ,坡角
,坡角![]() 為30°;改造后的斜坡式自動(dòng)扶梯的坡角
為30°;改造后的斜坡式自動(dòng)扶梯的坡角![]() 為15°,改造后的斜坡式自動(dòng)扶梯水平距離增加了
為15°,改造后的斜坡式自動(dòng)扶梯水平距離增加了![]() ,請你計(jì)算
,請你計(jì)算![]() 的長度,(結(jié)果精確到
的長度,(結(jié)果精確到![]() ,參考數(shù)據(jù):
,參考數(shù)據(jù):![]() )
)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在菱形ABCD中,∠B=60°,AB=2,M為邊AB的中點(diǎn),N為邊BC上一動(dòng)點(diǎn)(不與點(diǎn)B重合),將△BMN沿直線MN折疊,使點(diǎn)B落在點(diǎn)E處,連接DE、CE,當(dāng)△CDE為等腰三角形時(shí),BN的長為_____.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,按以下步驟作圖:①以A為圓心,AB長為半徑畫弧,交邊AD于點(diǎn);②再分別以B,F為圓心畫弧,兩弧交于平行四邊形ABCD內(nèi)部的點(diǎn)G處;③連接AG并延長交BC于點(diǎn)E,連接BF,若BF=3,AB=2.5,則AE的長為( )
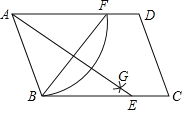
A.2B.4C.8D.5
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知拋物線y=ax2+bx+c(a≠0)的對稱軸是![]() ,且經(jīng)過A(﹣4,0),C(0,2)兩點(diǎn),直線l:y=kx+t(k≠0)經(jīng)過A,C.
,且經(jīng)過A(﹣4,0),C(0,2)兩點(diǎn),直線l:y=kx+t(k≠0)經(jīng)過A,C.
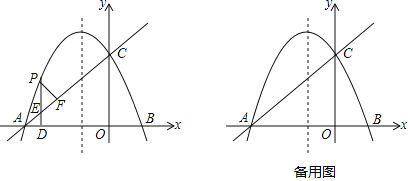
(1)求拋物線和直線l的解析式;
(2)點(diǎn)P是直線AC上方的拋物線上一個(gè)動(dòng)點(diǎn),過點(diǎn)P作PD⊥x軸于點(diǎn)D,交AC于點(diǎn)E,過點(diǎn)P作PF⊥AC,垂足為F,當(dāng)△PEF≌△AED時(shí),求出點(diǎn)P的坐標(biāo);
(3)在拋物線的對稱軸上是否存在點(diǎn)Q,使△ACQ為等腰三角形?若存在,直接寫出所有滿足條件的Q點(diǎn)的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】2019年12月16日揚(yáng)州首批為民服務(wù)5G站點(diǎn)正式上線,自此有了5G網(wǎng)絡(luò).5G網(wǎng)絡(luò)峰值速率為4G網(wǎng)絡(luò)峰值速率的10倍,在峰值速率下傳輸500兆數(shù)據(jù),5G網(wǎng)絡(luò)比4G網(wǎng)絡(luò)快45秒,求這兩種網(wǎng)絡(luò)的峰值速率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
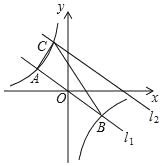
【題目】如圖,在平面直角坐標(biāo)系中,直線l1:y=﹣![]() x與反比例函數(shù)y=
x與反比例函數(shù)y=![]() 的圖象交于A,B兩點(diǎn)(點(diǎn)A在點(diǎn)B左側(cè)),已知A點(diǎn)的縱坐標(biāo)是2:
的圖象交于A,B兩點(diǎn)(點(diǎn)A在點(diǎn)B左側(cè)),已知A點(diǎn)的縱坐標(biāo)是2:
(1)求反比例函數(shù)的表達(dá)式;
(2)將直線l1:y=﹣![]() x向上平移后的直線l2與反比例函數(shù)y=
x向上平移后的直線l2與反比例函數(shù)y=![]() 在第二象限內(nèi)交于點(diǎn)C,如果△ABC的面積為30,求平移后的直線l2的函數(shù)表達(dá)式.
在第二象限內(nèi)交于點(diǎn)C,如果△ABC的面積為30,求平移后的直線l2的函數(shù)表達(dá)式.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com