（本題滿分6分）
（1）如圖1，正方形ABCD和CEFG的邊長分別為m、n，用含m、n的代數式表示△AEG的面積。
（2）如圖2，正方形ABCD和CEFG的邊長分別為m、n，用含m、n的代數式表示△DBF的面積。
（3）如圖，正方形ABCD、正方形CEFG和正方形MNHF的位置如圖所示，點G在線段AN上，已知正方形CEFG的邊長為6，則△AEN的面積為 （請直接寫出結果，不需要過程）
【解析】
試題分析：（1）利用面積的和差計算：△AEG的面積等于四邊形ABEG的面積減去三角形ABE的面積，而四邊形ABEG的面積等于梯形ABCG的面積與三角形CEG的面積和，于是得到△AEG的面積=
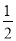（n+m）m+
－
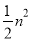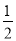（m+n）m化簡即可；（2）與（1）的方法一樣求解；（3）利用（1）、（2）的結論求出△AEG的面積和△GEN的面積，然后把它們相加即可.
試題解析：【解析】
（1）△AEG的面積=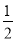
（m+n）n+
-
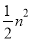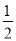n（m+n） =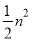
（2）△DBF的面積=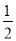
（m+n）n+
-
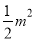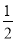n（m+n）= 
.
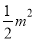（3）連接GE,如圖3，由（1）可得△AEG的面積=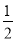
×36=18，由（2）可得：三角形GEN的面積為
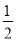×36=18所以，△AEN的面積=18+18=36，
考點：列代數式
各地期末復習特訓卷系列答案
小博士期末闖關100分系列答案科目：初中數學 來源：2014-2015學年江蘇省揚州市江都十校八年級12月聯誼月考數學試卷（解析版） 題型：解答題
（本題12分）如圖①所示，直線L：
與
軸負半軸、
軸正半軸分別交于A、B兩點。
（1）當OA=OB時，試確定直線L的解析式；
（2）在（1）的條件下，如圖②所示，設Q為AB延長線上一點，作直線OQ，過A、B兩點分別作AM⊥OQ于M，BN⊥OQ于N，試說明MN=AM+BN。
（3）當
取不同的值時，點B在
軸正半軸上運動，分別以OB、AB為邊，點B為直角頂點在第一、二象限內作等腰直角△OBF和等腰直角△ABE，連EF交
軸于P點，如圖③。
問：當點B在 y軸正半軸上運動時，試猜想PB的長是否為定值，若是，請求出其值，若不是，說明理由。
查看答案和解析>>
科目：初中數學 來源：2014-2015學年江蘇省揚州市江都十校八年級12月聯誼月考數學試卷（解析版） 題型：選擇題
已知點P在第四象限，且到x軸的距離為3，到y軸的距離為2，則點P的坐標為（ ）
A．（－2，3） B．（2，－3） C．（3，－2） D．（－3，2）
查看答案和解析>>
科目：初中數學 來源：2014-2015學年江蘇省無錫市七年級上學期期中考試數學試卷（解析版） 題型：選擇題
a為有理數，定義運算符號“※”：當a＞－2時，※a＝－a；當a＜－2時，※a＝a；當a＝－2時，※a＝0．根據這種運算，則※[4＋※（2－5）]的值為--------------（ ）
A．1 B．－1 C．7 D．－7
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
軸對稱的點的坐標為 ．
， 
，
的值是
，則代數式
的值為 
，求代數式
的值.