已知關于x的一元二次方程x2-4x+1-2k=0有兩個不等的實根,
(1)求k的取值范圍;
(2)若k取小于1的整數,且此方程的解為整數,則求出此方程的兩個整數根;
(3)在(2)的條件下,二次函數y=x2-4x+1-2k與x軸交于A、B兩點(A點在B點的左側),D點在此拋物線的對稱軸上,若
∠DAB=60°,求D點的坐標.
解:(1)∵關于x的一元二次方程x
2-4x+1-2k=0有兩個不等的實根,
∴△=(-4)
2-4×1×(1-2k)=12+8k>0,
解得,k>-

;
(2)∵k取小于1的整數,
∴k=-1或0,
①當k=-1時,方程為x
2-4x+3=0,
即(x-2)
2=1,
∴x-2=1或x-2=-1,
解得x
1=3,x
2=1,
②當k=0時,方程為x
2-4x+1=0,
即(x-2)
2=3,
∵方程的解為整數,
∴k=0不符合,
∴k=-1,此時方程的兩個整數根是x
1=3,x
2=1;
(3)如圖所示,根據(2),二次函數解析式為,y=x
2-4x+3,
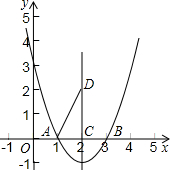
∴點A、B的坐標分別為A(1,0),B(3,0),
∴對稱軸為x=2,
∴AC=

(3-1)=1,
∵∠DAB=60°,
∴AD=2AC=2,
∴CD=

=

=

,
當點D在AB的上方時,坐標為(2,

),在AB的下方時,坐標為(2,-

),
∴點D的坐標為(2,

)或(2,-

).
分析:(1)根據根的判別式,有兩個不等的實根,根的判別式△=b
2-4ac>0列出關于k的不等式12+8k>0,求解即可得到k的取值范圍;
(2)利用(1)中k的取值范圍求得k的整數解,然后將其代入關于x的一元二次方程x
2-4x+1-2k=0并整理,再根據配方法進行求解;
(3)先求出二次函數的解析式,然后求出拋物線與x軸的交點,從而得到對稱軸的解析式以及AB的長度,再根據∠DAB=60°求出點D到x軸的距離,然后根據點D在AB的上方與下方兩種情況討論得解.
點評:本綜合考查了根的判別式,一元二次方程的解法以及二次函數的性質,拋物線與x軸的交點情況,綜合性較強,但難度不是很大,根據整數根求出k的值是解題的關鍵.

 ;
;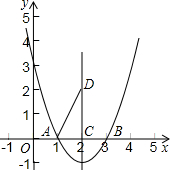
 (3-1)=1,
(3-1)=1, =
= =
= ,
, ),在AB的下方時,坐標為(2,-
),在AB的下方時,坐標為(2,- ),
), )或(2,-
)或(2,- ).
).

 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案 .
. .
.