Question

【題目】在ABCD中，AB=2BC=4，E、F分別為AB、CD的中點

①求證：△ADE≌△CBF；

②若四邊形DEBF為菱形，求四邊形ABCD的面積．

Answer 1

【答案】（1）證明見解析；（2）4 ．

【解析】試題分析：

試題解析：(1)根據平行四邊形性質，可得三角形對應角相等，對應邊相等，SAS易得△ADE≌△CBF.

(2)連接BD, ABD是30°的直角三角形，所以可求得ABD的面積，因為E,F是中點，所以所以利用等面積法，可知平行四邊形的面積.

試題解析：

①證明：∵四邊形ABCD是平行四邊形，

∴AD=BC，AB=CD，∠A=∠C，

∵E、F分別為AB、CD的中點，

∵AE=EB，DF=FC，

∴AE=CF，

在△ADE和△CBF中，

,

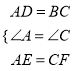∴△ADE≌△CBF，

②連接BD，

由①有AE=EB，

∵四邊形DEBF是菱形，

∴DE=EB=AE，

∴△ADB是直角三角形，

在RT△ADB中，∵∠ADB=90°，AD=BC=2，AB=4，

∴BD==，

∵四邊形ABCD是平行四邊形，

∴S平行四邊形ABCD=2S△ADB=2××2×2=4 ．