
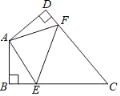
【題目】如圖, ![]() 是等邊三角形,點
是等邊三角形,點 ![]() 在同一條直線上,且
在同一條直線上,且 ![]() .
.
(1)請直接寫出圖中相似的三角形;
(2)探究 ![]() 之間的關系,并說明理由.
之間的關系,并說明理由.
【答案】
(1)解:△DAE∽△DBA∽△ACE
(2)解:∵△ABC是等邊三角形,∴∠ABC=∠ACB=∠BAC=60°.
∴∠D+∠DAB=∠ABC= 60°,∠E+∠CAE=∠ACB=60°.
∵∠DAE=120°,
∴∠DAB+∠CAE=60°.
∴∠D=∠CAE,∠E=∠DAB.
∴△DBA∽△ACE.
∴DB∶AC=AB∶EC.
得DB×EC =AB×AC
∵AB=AC=BC,
∴BC2=DBEC.
【解析】第1小題,圖中的相似三角形有:△DAE∽△DBA∽△ACE;第2小題,根據△ABC是等邊三角形得到∠ABC=∠ACB=∠BAC=60°.再由已知條件得到
△DBA∽△ACE,結論得證。
【考點精析】根據題目的已知條件,利用等邊三角形的性質和相似三角形的性質的相關知識可以得到問題的答案,需要掌握等邊三角形的三個角都相等并且每個角都是60°;對應角相等,對應邊成比例的兩個三角形叫做相似三角形.


科目:初中數學 來源: 題型:
【題目】你能化簡(x-1)(x99+x98+x97+…+x+1)嗎?遇到這樣的問題,我們可以先思考一下,從簡單的情形入手,然后歸納出一些方法.
(1)分別化簡下列各式:
①(x-1)(x+1)=___________;
②(x-1)(x2+x+1)=___________;
③(x-1)(x3+x2+1)=___________;
……
由此我們可以得到:(x-1)(x99+x98+x97+…+x+1)=________________.
(2)請你利用上面的結論計算:
299+298+297+…+2+1.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示的函數圖象反映的過程是:李大爺每天早上都到公園鍛煉,他從家去公園鍛煉一會兒,又去了菜市場后馬上回家,其中![]() 表示時間,
表示時間,![]() 表示李大爺離他家的距離。
表示李大爺離他家的距離。
(1)李大爺家到公園的距離是多少千米,他在公園銀煉了多少小時;
(2)李大爺從菜市場回家的平均速度;
(3)李大爺從家到菜市場的平均速度。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】你知道為什么任何無限循環小數都可以寫成分數形式嗎?下面的解答會告訴你方法.
(1)閱讀下列材料:
問題:利用一元一次方程將![]() 化成分數.
化成分數.
解:設![]() .
.
方程兩邊都乘以10,可得![]() .
.
由![]() 和
和![]() ,可得
,可得![]() 即
即![]() .(請你體會將方程兩邊都乘以10起到的作用)
.(請你體會將方程兩邊都乘以10起到的作用)
解得![]() ,即
,即![]() .
.
填空:將0.![]() 寫成分數形式為 .
寫成分數形式為 .
(2)請你仿照上述方法把小數1.![]() 化成分數,要求寫出利用一元一次方程進行解答的過程.
化成分數,要求寫出利用一元一次方程進行解答的過程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數 ![]() 的
的 ![]() 與
與 ![]() 的部分對應值如下表:
的部分對應值如下表:
| … | -1 | 0 | 1 | 3 | … |
| … | -3 | 1 | 3 | 1 | … |
則下列判斷中正確的是( )
A.拋物線開口向上
B.拋物線與 ![]() 軸交于負半軸
軸交于負半軸
C.當 ![]() 時,
時, ![]()
D.方程 ![]() 的正根在3與4之間
的正根在3與4之間
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】九年三班的小雨同學想了解本校九年級學生對哪門課程感興趣,隨機抽取了部分九年級學生進行調查(每名學生必只能選擇一門課程).將獲得的數據整理繪制如下兩幅不完整的統計圖.

據統計圖提供的信息,解答下列問題:
(1)在這次調查中一共抽取了 名學生,m的值是 .
(2)請根據據以上信息直在答題卡上補全條形統計圖;
(3)扇形統計圖中,“數學”所對應的圓心角度數是 度;
(4)若該校九年級共有1000名學生,根據抽樣調查的結果,請你估計該校九年級學生中有多少名學生對數學感興趣.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】己知⊙O的半徑為 ![]() ,弦AB=2,以AB為底邊,在圓內畫⊙0的內接等腰△ABC,則底邊AB邊上的高CD長為( )
,弦AB=2,以AB為底邊,在圓內畫⊙0的內接等腰△ABC,則底邊AB邊上的高CD長為( )
A.![]() +1
+1
B.![]() ﹣1
﹣1
C.![]() 或
或 ![]() ﹣1
﹣1
D.![]() +1或
+1或 ![]() +1
+1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,∠BAD=130°,∠B=∠D=90°,點E,F分別是線段BC,DC上的動點.當△AEF的周長最小時,則∠EAF的度數為( )
A. 90°B. 80°C. 70°D. 60°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市道路美化工程招標,經測算:甲隊 12 天完成的工程量是乙隊 9 天完成的工程量的2 倍,甲隊干 20 天比乙隊干 15 天多完成的工程量占總工程量的![]() .
.
(1)求甲、乙兩隊一天各完成此項工程的量?
(2)甲隊施工一天需付工程款 1.5 萬元,乙隊施工一天需付工程款 0.8 萬元,若要求完成此項工程的工程款不超過 81 萬元,則乙隊最少施工多少天?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com