
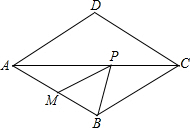
 如圖,菱形ABCD中,∠BAD=60°,M是AB的中點,P是對角線AC上的一個動點,若PM+PB的最小值是
如圖,菱形ABCD中,∠BAD=60°,M是AB的中點,P是對角線AC上的一個動點,若PM+PB的最小值是| 3 |
 解:如圖,∵四邊形ABCD是菱形,
解:如圖,∵四邊形ABCD是菱形,| 3 |
| 3 |
| 3 |
| DM |
| sin60° |
| ||||
|


科目:初中數學 來源: 題型:
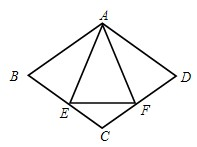 26、已知:如圖,菱形ABCD中,E,F分別是CB,CD上的點,且BE=DF.
26、已知:如圖,菱形ABCD中,E,F分別是CB,CD上的點,且BE=DF.查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,菱形ABCD中,∠A=60°,AB=2,動點P從點B出發,以每秒1個單位長度的速度沿B→C→D向終點D運動.同時動點Q從點A出發,以相同的速度沿A→D→B向終點B運動,運動的時間為x秒,當點P到達點D時,點P、Q同時停止運動,設△APQ的面積為y,則反映y與x的函數關系的圖象是( )
如圖,菱形ABCD中,∠A=60°,AB=2,動點P從點B出發,以每秒1個單位長度的速度沿B→C→D向終點D運動.同時動點Q從點A出發,以相同的速度沿A→D→B向終點B運動,運動的時間為x秒,當點P到達點D時,點P、Q同時停止運動,設△APQ的面積為y,則反映y與x的函數關系的圖象是( )A、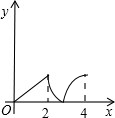 | B、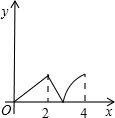 | C、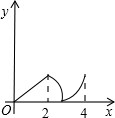 | D、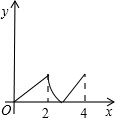 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com