
【題目】八年級數學教師邱龍從家里出發,駕車去離家![]() 的風景區度假,出發一小時內按原計劃的速度勻速行駛,一小時后以原速的1.5倍勻速行駛,并提前40分鐘到達風景區;第二天返回時以去時原計劃速度的1.2倍行駛回到家里.那么來回行駛時間相差_________分鐘.
的風景區度假,出發一小時內按原計劃的速度勻速行駛,一小時后以原速的1.5倍勻速行駛,并提前40分鐘到達風景區;第二天返回時以去時原計劃速度的1.2倍行駛回到家里.那么來回行駛時間相差_________分鐘.
科目:初中數學 來源: 題型:
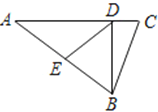
【題目】如圖,在△ABC中,AC=21,BC=13,D是AC邊上一點,BD=12,AD=16.
(1)求證:BD⊥AC.
(2)若E是邊AB上的動點,求線段DE的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
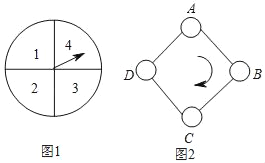
【題目】如圖1,是一個材質均勻可自由轉動的轉盤,轉盤的四個扇形面積相等,分別有數字1,2,3,4.如圖2,正方形ABCD頂點處各有一個圈.跳圈游戲的規則為:游戲者每轉動轉盤一次,當轉盤停止運動時,指針所落扇形中的數字是幾(當指針落在四個扇形的交線上時,重新轉動轉盤),就沿正方形的邊順時針方向連續跳幾個邊長.
如:若從圖A起跳,第一次指針所落扇形中的數字是3,就順時針連線跳3個邊長,落到圈D;若第二次指針所落扇形中的數字是2,就從D開始順時針續跳2個邊長,落到圈B;……設游戲者從圈A起跳.
(1)嘉嘉隨機轉一次轉盤,求落回到圈A的概率P1;
(2)琪琪隨機轉兩次轉盤,用列表法求最后落回到圈A的概率P2,并指出她與嘉嘉落回到圈A的可能性一樣嗎?
查看答案和解析>>
科目:初中數學 來源: 題型:
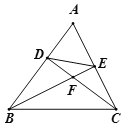
【題目】如圖,在△ABC中,點D,E分別在邊AB,AC上,且BE平分∠ABC,∠ABE=∠ACD,BE,CD交于點F.
(1)求證: ![]() ;
;
(2)請探究線段DE,CE的數量關系,并說明理由;
(3)若CD⊥AB,AD=2,BD=3,求線段EF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知反比例函數y=![]() (k≠0)的圖象經過點B(3,2),點B與點C關于原點O對稱,BA⊥x軸于點A,CD⊥x軸于點D.
(k≠0)的圖象經過點B(3,2),點B與點C關于原點O對稱,BA⊥x軸于點A,CD⊥x軸于點D.
(1)求這個反比函數的表達式;
(2)求△ACD的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在菱形![]() 中,點
中,點![]() 是邊
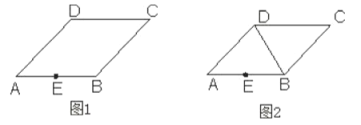
是邊![]() 的中點,試分別在下列兩個圖形中按要求使用無刻度的直尺畫圖.
的中點,試分別在下列兩個圖形中按要求使用無刻度的直尺畫圖.
(1)在圖1中,過點![]() 畫
畫![]() 的平行線;
的平行線;
(2)在圖2中,連接![]() ,在
,在![]() 上找一點
上找一點![]() ,使點
,使點![]() 到點
到點![]() ,
,![]() 的距離之和最短.
的距離之和最短.
查看答案和解析>>
科目:初中數學 來源: 題型:
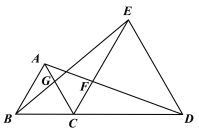
【題目】如圖,點C為線段BD上一點,△ABC、△CDE都是等邊三角形.AD與CE交于點F,BE與AC相交于點G.
(1)求證:△ACD≌△BCE;
(2)若CF+CG=8,BD=18,求△ACD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】自主學習,請閱讀下列解題過程.
解一元二次不等式:![]() >0.
>0.
解:設![]() =0,解得:
=0,解得:![]() =0,
=0,![]() =5,則拋物線y=
=5,則拋物線y=![]() 與x軸的交點坐標為(0,0)和(5,0).畫出二次函數y=
與x軸的交點坐標為(0,0)和(5,0).畫出二次函數y=![]() 的大致圖象(如圖所示),由圖象可知:當x<0,或x>5時函數圖象位于x軸上方,此時y>0,即
的大致圖象(如圖所示),由圖象可知:當x<0,或x>5時函數圖象位于x軸上方,此時y>0,即![]() >0,所以,一元二次不等式
>0,所以,一元二次不等式![]() >0的解集為:x<0或x>5.
>0的解集為:x<0或x>5.
通過對上述解題過程的學習,按其解題的思路和方法解答下列問題:
(1)上述解題過程中,滲透了下列數學思想中的 和 .(只填序號)
①轉化思想 ②分類討論思想 ③數形結合思想
(2)一元二次不等式![]() <0的解集為 .
<0的解集為 .
(3)用類似的方法解一元二次不等式:![]() >0.
>0.
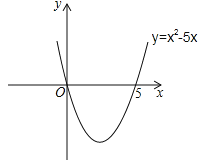
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com