
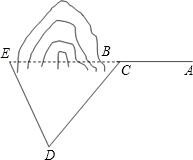
 需寫出結論.)
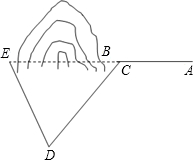
需寫出結論.)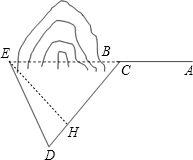 解:(1)作EH⊥DC于點H,
解:(1)作EH⊥DC于點H, x,
x, x,
x, x,
x, x+x=500,
x+x=500, -250,
-250, -500.
-500.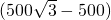 (米).
(米).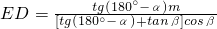 ,
, ,
,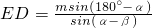 ,等等.
,等等. x,又在△EHC中,∠EHC=90°,∠ECD=180-∠ACD=45°,CH=EH=
x,又在△EHC中,∠EHC=90°,∠ECD=180-∠ACD=45°,CH=EH= x,列出等式,解出x、2x即可;
x,列出等式,解出x、2x即可;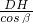 ,DH=
,DH= ,tg(180°-α)=
,tg(180°-α)=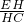 ,HC=m-DH=m-cosβ•DE,所以,DE=
,HC=m-DH=m-cosβ•DE,所以,DE=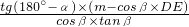 ,整理可得,ED=
,整理可得,ED=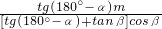 .
.

 一線名師提優試卷系列答案
一線名師提優試卷系列答案 陽光試卷單元測試卷系列答案
陽光試卷單元測試卷系列答案科目:初中數學 來源: 題型:
 需寫出結論.)
需寫出結論.)查看答案和解析>>
科目:初中數學 來源:2007年上海市寶山區中考數學一模試卷(解析版) 題型:解答題
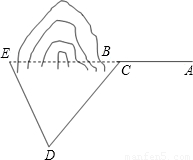
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com