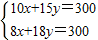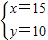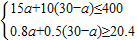【答案】
分析:(1)等量關系為:10輛A轎車的價錢+15輛B轎車的價錢=300萬元;8輛A轎車的價錢+18輛B轎車的價錢=300萬元;
(2)根據(1)中求出AB轎車的單價,然后根據關鍵語“用不超過400萬元購進A、B兩種型號轎車共30輛,且這兩種轎車全部售出后總獲利不低于20.4萬元”列出不等式組,判斷出不同的購車方案,進而求出不同方案的獲利的多少.
解答:解:(1)設A型號的轎車每輛為x萬元,B型號的轎車每輛為y萬元.
根據題意得
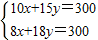
解得
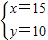
答:A、B兩種型號的轎車每輛分別為15萬元、10萬元;
(2)設購進A種型號轎車a輛,則購進B種型號轎車(30-a)輛.
根據題意得
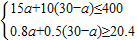
解此不等式組得18≤a≤20.
∵a為整數,∴a=18,19,20.
∴有三種購車方案.
方案一:購進A型號轎車18輛,購進B型號轎車12輛;
方案二:購進A型號轎車19輛,購進B型號車輛11輛;
方案三:購進A型號轎車20輛,購進B型號轎車10輛.
汽車銷售公司將這些轎車全部售出后:
方案一獲利18×0.8+12×0.5=20.4(萬元);
方案二獲利19×0.8+11×0.5=20.7(萬元);
方案三獲利20×0.8+10×0.5=21(萬元).
答:有三種購車方案,在這三種購車方案中,汽車銷售公司將這些轎車全部售出后分別獲利為20.4萬元,20.7萬元,21萬元.
點評:此題是典型的數學建模問題,要先將實際問題轉化為列方程組和列不等式組解應用題.