
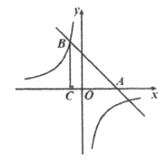
【題目】如圖,在平面直角坐標系xOy中,直線![]() 與x軸交于點A,與雙曲線
與x軸交于點A,與雙曲線![]() 的一個交點為B(-1,4).
的一個交點為B(-1,4).
(1)求直線與雙曲線的表達式;
(2)過點B作BC⊥x軸于點C,若點P在雙曲線![]() 上,且△PAC的面積為4,求點P的坐標.
上,且△PAC的面積為4,求點P的坐標.
 寒假創新型自主學習第三學期寒假銜接系列答案
寒假創新型自主學習第三學期寒假銜接系列答案科目:初中數學 來源: 題型:
【題目】已知:如圖,在△ABC中,AB=AC,以AC為直徑的⊙O與BC交于點D,DE⊥AB,垂足為E,ED的延長線與AC的延長線交于點F。

(1)求證:DE是⊙O的切線;
(2)若⊙O的半徑為4,BE=2,求∠F的度數。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 (用如圖所示的曲尺形框框(有三個方向),可以套住下表中的三個數,設被框住的三個數中(第一個框框住的最小的數為a、第二個框框住的最小的數為b、第三個框框住的最小的數為c).
(1)第一個框框住的三個數中最小的數為a,三個數的和是: ;第二個框框住的三個數中最小的數為b,三個數的和是: ;第三個框框住的三個數中最小的數為c,三個數的和是: ;
(2)這三個框框住的數的和能是48嗎?,能,求出最小的數a、b、c的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在下列四項調查中,方式正確的是![]()
![]()
A. 了解本市中學生每天學習所用的時間,采用全面調查的方式
B. 為保證運載火箭的成功發射,對其所有的零部件采用抽樣調查的方式
C. 了解某市每天的流動人口數,采用全面調查的方式
D. 了解全市中學生的視力情況,采用抽樣調查的方式
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是“用三角板畫圓的切線”的畫圖過程.
如圖1,已知圓上一點A,畫過A點的圓的切線.
![]()

畫法:(1)如圖2,將三角板的直角頂點放在圓上任一點C(與點A不重合)處,使其一直角邊經過點A,另一條直角邊與圓交于B點,連接AB;
(2)如圖3,將三角板的直角頂點與點A重合,使一條直角邊經過點B,畫出另一條直角邊所在的直線AD.
所以直線AD就是過點A的圓的切線.
請回答:該畫圖的依據是_______________________________________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】兩輛汽車從相距84 km的兩地同時出發相向而行,甲車的速度比乙車的速度快20 km/h,半小時后兩車相遇.
(1)求乙車的速度是每小時多少千米?
(2)甲車的速度是_______ km/h;
(3)兩車相遇時,甲車比乙車多行駛________千米.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角坐標系中,點A、B的坐標分別為(1,4)和(3,0),點C是y軸上的一個動點,且A、B、C三點不在同一條直線上,當△ABC的周長最小時,點C的坐標是( )
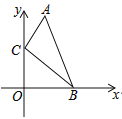
A. (0,0); B. (0,1); C. (0,2); D. (0,3).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數軸是一個非常重要的數學工具,通過它把數和數軸上的點建立起對應關系,揭示了數與點之間的內在聯系,它是“數形結合”的基礎.已知數軸上有點A和點B,點A和點B分別表示數-20和40,請解決以下問題:
(1)請畫出數軸,并標明A、B兩點;
(2)若點P、Q分別從點A、點B同時出發,相向而行,點P、Q移動的速度分別為每秒4個單位長度和2個單位長度.問:當P、Q相遇于點C時,C所對應的數是多少?
(3)若點P、Q分別從點A、點B同時出發,沿x軸正方向同向而行,點P、Q移動的速度分別為每秒4個單位長度和2個單位長度.問:當P、Q相遇于點D時,D所對應的數是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com