
【題目】2019年3月15日,我國“兩會”落下帷幕.13天時間里,來自各地的5000余名代表、委員聚于國家政治中心,共議國家發展大計.某校初三(3)班張老師為了了解同學們對“兩會”知識的知曉情況,進行了一次小測試,測試滿分100分.其中
A組同學的測試成績分別為:91 91 86 93 85 89 89 88 87 91
B組同學的測試成績分別為:88 97 88 85 86 94 84 83 98 87
根據以上數據,回答下列問題:
(1)完成下表:
組別 | 平均數 | 中位數 | 眾數 | 方差 |
A組 | 89 | 89 | b | c |
B組 | 89 | a | 88 | 26.2 |
其中a= ,b= ,c= ,
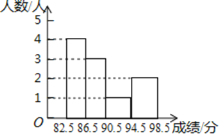
(2)張老師將B組同學的測試成績分成四組并繪制成如圖所示頻數分布直方圖(不完整),請補全;
(3)根據以上分析,你認為 組(填“A”或“B”)的同學對今年“兩會”知識的知曉情況更好一些,請寫出你這樣判斷的理由(至少寫兩條):① ② .

【答案】(1)87.5,91,5.8;(2)詳見解析;(3)A;A組的中位數大于B組;在兩組平均數相同的情況下,A組的方差小于B組,A組波動小,成績穩定.
【解析】
(1)根據題目中的數據可以將A組和B組的成績按照從小到大排列,從而可以的到a、b、c的值;
(2)根據題意和B組的數據,可以將頻數分布直方圖補充完整;
(3)根據表格中的數據可以解答本題,注意寫理由時,主要合理即可,本題答案不唯一.
(1)A組同學的測試成績按照從小到大排列是:85,86,87,88,89,89,91,91,91,93,
B組同學的測試成績按照從小到大排列是:83,84,85,86,87,88,88,94,97,98,
則a=(87+88)÷2=87.5,
b=91,
c=![]() =5.8,
=5.8,
故答案為:87.5,91,5.8;
(2)∵B組同學的測試成績按照從小到大排列是:83,84,85,86,87,88,88,94,97,98,
∴90.5≤x<94.5的有1人,94.5≤x<98.5的有2人,
補全的頻數分布直方圖如圖所示;
(3)根據以上分析, A組的同學對今年“兩會”知識的知曉情況更好一些,
理由:①A組的中位數大于B組;②在兩組平均數相同的情況下,A組的方差小于B組,A組波動小,成績穩定;
故答案為:A;A組的中位數大于B組;在兩組平均數相同的情況下,A組的方差小于B組,A組波動小,成績穩定.


科目:初中數學 來源: 題型:
【題目】設等邊三角形的內切圓半徑為![]() 外接圓半徑為
外接圓半徑為![]() ,平面內任意一點
,平面內任意一點![]() 到等邊三角形中心的距離為
到等邊三角形中心的距離為![]() 若滿足
若滿足![]() 則稱點
則稱點![]() 叫做等邊三角形的中心關聯點.在平面直角坐標系
叫做等邊三角形的中心關聯點.在平面直角坐標系![]() 中,等邊
中,等邊![]() 的三個頂點的坐標分別為
的三個頂點的坐標分別為![]() .
.
(1)①等邊![]() 中心的坐標為 ;
中心的坐標為 ;
②已知點![]() 在
在![]() 中,是等邊
中,是等邊![]() 的中心關聯點的是 ;
的中心關聯點的是 ;
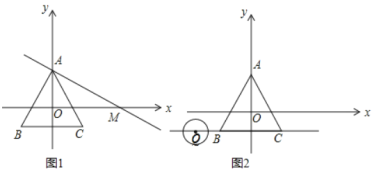
(2)如圖1,過點![]() 作直線交
作直線交![]() 軸正半軸于
軸正半軸于![]() 使
使![]() .
.
①若線段![]() 上存在等邊
上存在等邊![]() 的中心關聯點
的中心關聯點![]() 求
求![]() 的取值范圍;
的取值范圍;
②將直線![]() 向下平移得到直線
向下平移得到直線![]() 當
當![]() 滿足什么條件時,直線
滿足什么條件時,直線![]() 上總存在等邊
上總存在等邊![]() 的中心關聯點;
的中心關聯點;
(3)如圖2,點![]() 為直線
為直線![]() 上一動點,
上一動點,![]() 的半徑為
的半徑為![]() 當
當![]() 從點
從點![]() 出發,以每秒
出發,以每秒![]() 個單位的速度向右移動,運動時間為
個單位的速度向右移動,運動時間為![]() 秒.是否存在某一時刻
秒.是否存在某一時刻![]() 使得
使得![]() 上所有點都是等邊
上所有點都是等邊![]() 的中心關聯點?如果存在,請直接寫出所有符合題意的
的中心關聯點?如果存在,請直接寫出所有符合題意的![]() 的值;如果不存在,請說明理由.
的值;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】初中學生對待學習的態度一直是教育工作者極為關注的一個問題.為此某市教育局對本市部分學校的八年級學生對待學習的態度進行了一次抽樣調查(把學習態度分為三個層級,A級:喜歡;B級:不太喜歡;C級:不喜歡),并將調查結果繪制成不完整的統計圖(如圖![]() ).請根據圖中提供的信息,解答下列問題:
).請根據圖中提供的信息,解答下列問題:
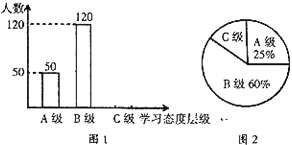
(1)此次抽樣調查中,共調查了_____名學生;
(2)將條形統計圖補充完整;
(3)求出扇形統計圖中![]() 級所占的圓心角的度數;
級所占的圓心角的度數;
(4)根據抽樣調查結果,請你估計該市近![]() 名初中生中大約有多少名學生學習態度達標.(達標包括
名初中生中大約有多少名學生學習態度達標.(達標包括![]() 級和
級和![]() 級)
級)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖, ![]() 是直線
是直線![]() 上的兩點,直線l1、l2的初始位置與直線
上的兩點,直線l1、l2的初始位置與直線![]() 重合將l1繞點
重合將l1繞點![]() 順時針以每秒10°的速度旋轉,將l2繞點B逆時針以每秒5°的速度旋轉,且兩條直線從重合位置同時開始旋轉,設旋轉時間為
順時針以每秒10°的速度旋轉,將l2繞點B逆時針以每秒5°的速度旋轉,且兩條直線從重合位置同時開始旋轉,設旋轉時間為![]() 秒(
秒(![]() 是正整數).當
是正整數).當![]() 時,設
時,設![]() 的交點為
的交點為![]() ;當
;當![]() 時,設
時,設![]() 的交點為
的交點為![]() ;當
;當![]() 時設
時設![]() 的交點為
的交點為![]() ……那么當
……那么當![]() 時,
時, ![]() 相交所得的鈍角是__________.當
相交所得的鈍角是__________.當![]() 落在
落在![]() 上方時,
上方時, ![]() 的最小值是__________.
的最小值是__________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在正方形ABCD外取一點E,連接AE、BE、DE.過點A作AE的垂線交DE于點P.若AE=AP=1,PB=![]() .下列結論:①△APD≌△AEB;②點B到直線AE的距離為
.下列結論:①△APD≌△AEB;②點B到直線AE的距離為![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+![]() .其中正確結論的序號是( )
.其中正確結論的序號是( )

A.①③④ B.①②⑤ C.③④⑤ D.①③⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
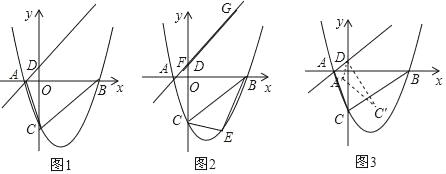
【題目】如圖1,拋物線y=![]() x2﹣
x2﹣![]() x﹣3,與x軸交于A和B兩點(點A在點B的左側),與y軸交于點C,過點A的直線與拋物線在第一象限的交點M的橫坐標為
x﹣3,與x軸交于A和B兩點(點A在點B的左側),與y軸交于點C,過點A的直線與拋物線在第一象限的交點M的橫坐標為![]() ,直線AM與y軸交于點D,連接BC、AC.
,直線AM與y軸交于點D,連接BC、AC.
(1)求直線AD和BC的解折式;
(2)如圖2,E為直線BC下方的拋物線上一點,當△BCE的面積最大時,一線段FG=4![]() (點F在G的左側)在直線AM上移動,順次連接B、E、F、G四點構成四邊形BEFG,請求出當四邊形BEFG的周長最小時點F的坐標;
(點F在G的左側)在直線AM上移動,順次連接B、E、F、G四點構成四邊形BEFG,請求出當四邊形BEFG的周長最小時點F的坐標;
(3)如圖3,將△DAC繞點D逆時針旋轉角度α(0°<α<180°),記旋轉中的三角形為△DA′C′,若直線A′C′分別與直線BC、y軸交于M、N,當△CMN是等腰三角形時,請直接寫出CM的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠的甲、乙兩個車間各生產了400個新款產品,為了檢驗甲、乙兩車間生產的同一款新產品的合格情況(尺寸范圍在165≤x<180為合格),分別從甲、乙兩個車間生產的產品中隨機各抽取了20個樣品迸行檢測,獲得了它們的數據(尺寸),并對數據進行了整理、描述和分析.下面給出了部分信息:
a.甲車間產品尺寸的扇形統計圖如下(數據分為6組:165≤x<170,170≤x<175,
175≤x<180,180≤x<185,185≤x<190,190≤x≤195):


b.甲車間生產的產品尺寸在175≤x<180這一組的是:
175 176 176 177 177 178 178 179 179
c.甲、乙兩車間生產產品尺寸的平均數、中位數、眾數如下:
車間 | 平均數 | 中位數 | 眾數 |
甲車間 | 178 | m | 183 |
乙車間 | 177 | 182 | 184 |
根據以上信息,回答下列問題:
(1)表中m的值為 ;
(2)此次檢測中,甲、乙兩車間生產的產品合格率更高的是 (填“甲”或“乙”),理由是 ;
(3)如果假設這個工廠生產的所有產品都參加了檢測,那么估計甲車間生產該款新產品中合格產品有 個.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() ,
,![]() ,
,![]() 是等圓,
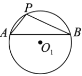
是等圓,![]() 內接于
內接于![]() ,點
,點![]() ,
,![]() 分別在
分別在![]() ,
,![]() 上.如圖,
上.如圖,
①以![]() 為圓心,
為圓心,![]() 長為半徑作弧交
長為半徑作弧交![]() 于點
于點![]() ,連接
,連接![]() ;
;
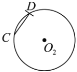
②以![]() 為圓心,
為圓心,![]() 長為半徑作弧交
長為半徑作弧交![]() 于點
于點![]() ,連接
,連接![]() ;
;
下面有四個結論:
①![]()
②![]()
③![]()
④![]()
所有正確結論的序號是( ).
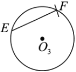
A.①②③④B.①②③C.②④D.②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合與實踐
背景閱讀 早在三千多年前,我國周朝數學家商高就提出:將一根直尺折成一個直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”.它被記載于我國古代著名數學著作《周髀算經》中,為了方便,在本題中,我們把三邊的比為3:4:5的三角形稱為(3,4,5)型三角形,例如:三邊長分別為9,12,15或3![]() ,4
,4![]() ,5
,5![]() 的三角形就是(3,4,5)型三角形,用矩形紙片按下面的操作方法可以折出這種類型的三角形.
的三角形就是(3,4,5)型三角形,用矩形紙片按下面的操作方法可以折出這種類型的三角形.
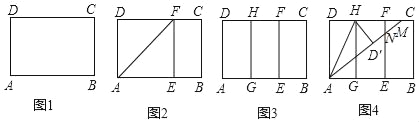
實踐操作 如圖1,在矩形紙片ABCD中,AD=8cm,AB=12cm.
第一步:如圖2,將圖1中的矩形紙片ABCD沿過點A的直線折疊,使點D落在AB上的點E處,折痕為AF,再沿EF折疊,然后把紙片展平.
第二步:如圖3,將圖2中的矩形紙片再次折疊,使點D與點F重合,折痕為GH,然后展平,隱去AF.
第三步:如圖4,將圖3中的矩形紙片沿AH折疊,得到△AD′H,再沿AD′折疊,折痕為AM,AM與折痕EF交于點N,然后展平.
問題解決
(1)請在圖2中證明四邊形AEFD是正方形.
(2)請在圖4中判斷NF與ND′的數量關系,并加以證明;
(3)請在圖4中證明△AEN(3,4,5)型三角形;
探索發現
(4)在不添加字母的情況下,圖4中還有哪些三角形是(3,4,5)型三角形?請找出并直接寫出它們的名稱.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com