如圖，在平行四邊形ABCD中，過點B作BE∥AC，在BG上取點E，連接DE交AC的延長線于點F．
（1）求證：DF=EF；
（2）如果AD=6，∠ADC=60°，AC⊥DC于點C，AC=2CF，求BE的長．
英才點津系列答案
紅果子三級測試卷系列答案科目：初中數學 來源：2016年初中畢業升學考試（甘肅蘭州卷）數學（解析版） 題型：填空題
?ABCD的對角線AC與BD相交于點O，且AC⊥BD，請添加一個條件： ，使得?ABCD為正方形．
查看答案和解析>>
科目：初中數學 來源：2016屆浙江省杭州市蕭山區九年級3月質檢數學試卷（解析版） 題型：解答題
如圖，△ABC和△DEF均是邊長為4的等邊三角形，△DEF的頂點D為△ABC的一邊BC的中點，△DEF繞點D旋轉，且邊DF、DE始終分別交△ABC的邊AB、AC于點H、G.圖中直線BC兩側的圖形關于直線BC成軸對稱.連結HH′、HG、GG′、H′G′，其中HH′、GG′分別交BC于點I、J.
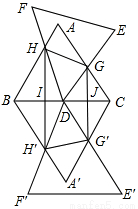
（1）求證：△DHB∽△GDC；
（2）設CG=x，四邊形HH′G′G的面積為y，
①求y關于x的函數解析式和自變量x的取值范圍；
②求當x為何值時，y的值最大，最大值為多少？
查看答案和解析>>
科目：初中數學 來源：2016屆浙江省杭州市蕭山區九年級3月質檢數學試卷（解析版） 題型：選擇題
在平面直角坐標系xOy中，經過點（sin45°,cos30°）的直線，與以原點為圓心，2為半徑的圓的位置關系是（ ）
A.相交 B.相切 C.相離 D.以上三者都有可能
查看答案和解析>>
科目：初中數學 來源：2016屆江蘇省九年級下第一次月考數學試卷（解析版） 題型：解答題
閱讀理【解析】
對于任意正實數a,b，
，
∴
，
∴a+b≥2
，當且僅當a=b時，等號成立．
結論：在a+b≥2（a,b均為正實數）中，若ab為定值p，則
，
當且僅當a=b，a+b有最小值
．
根據上述內容，回答下列問題：
（1）若x＞0，只有當x= 時，
有最小值 ．
（2）探索應用：如圖，已知A(-2,0)，B(0,-3)，點P為雙曲線
上的任意一點，過點P作PC⊥x軸于點C，PD⊥y軸于點D．求四邊形ABCD面積的最小值，并說明此時四邊形ABCD的形狀．
（3）已知x＞0，則自變量x為何值時，函數
取到最大值，最大值為多少？
查看答案和解析>>
科目：初中數學 來源：2016屆江蘇省九年級下第一次月考數學試卷（解析版） 題型：填空題
若正整數n使得在計算n+（n+1）+（n+2）的過程中，個數位上均不產生進為現象，則稱n為“本位數”，例如2和30是“本位數”，而5和91不是“本位數”.現從所有大于0且小于100的“本位數”中，隨機抽取一個數，抽到奇數的概率為 .
查看答案和解析>>
科目：初中數學 來源：2016屆江蘇省南京市秦淮區中考一模數學試卷（解析版） 題型：解答題
在平面幾何的學習過程中，我們經常會研究角和線之間的關系．
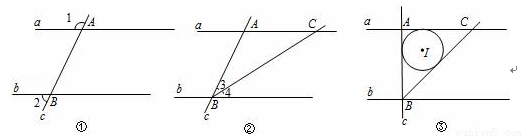
（1）如圖①，直線a、b被直線c所截，交點分別為A、B．當∠1、∠2滿足數量關系 時，a∥b；
（2）如圖②，在（1）中，作射線BC，與直線a的交點為C，當∠3、∠4滿足何種數量關系時，AB=AC？證明你的結論；
（3）如圖③，在（2）中，若∠BAC=90°，AB=2，⊙I為△ABC的內切圓．
①求⊙I的半徑；
②P為直線a上一點，若⊙I上存在兩個點M、N，使∠MPN=60°，直接寫出AP長度的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
．
得 ．