若兩個三角形相似,其中一個三角形的三條邊分別是6、8、10,另一個三角形的最大邊長是5,則另一個三角形的最短邊長及面積分別是________,________.
3 6
分析:由三角形的三條邊分別是6、8、10,根據勾股定理的逆定理,即可得此三角形是直角三角形,又由兩個三角形相似,另一個三角形的最大邊長是5,根據相似三角形的對應邊成比例,即可求得另一個三角形的最短邊長,繼而求得第三邊,則可求得其面積.
解答:∵一個三角形的三條邊分別是6、8、10,
又∵10
2=6
2+8
2,
∴這個三角形是直角三角形,
設另一個三角形的最短邊長為x,
∵兩個三角形相似,另一個三角形的最大邊長是5,
∴
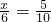
,
∴x=3,
∴此三角形也是直角三角形,第三邊為4,
∴此三角形的面積為:

×3×4=6.
故答案為:3,6.
點評:此題考查了相似三角形的性質與勾股定理的逆定理,以及直角三角形的面積的求解方法.此題難度不大,解題的關鍵是注意相似三角形的對應邊成比例.

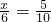 ,
, ×3×4=6.
×3×4=6.

 新思維假期作業暑假吉林大學出版社系列答案
新思維假期作業暑假吉林大學出版社系列答案