
【題目】為建設最美恩施,一旅游投資公司擬定在某景區用茶花和月季打造一片人工花海,經市場調查,購買![]() 株茶花與
株茶花與![]() 株月季的費用相同,購買
株月季的費用相同,購買![]() 株茶花與
株茶花與![]() 株月季共需
株月季共需![]() 元.
元.
(1)求茶花和月季的銷售單價;
(2)該景區至少需要茶花月季共![]() 株,要求茶花比月季多
株,要求茶花比月季多![]() 株,但訂購兩種花的總費用不超過
株,但訂購兩種花的總費用不超過![]() 元,該旅游投資公司怎樣購買所需總費用最低,最低費用是多少.
元,該旅游投資公司怎樣購買所需總費用最低,最低費用是多少.
【答案】(1)茶花價格為20元/株,月季價格為15元/株;(2)當![]() 時,
時,![]() 元
元
【解析】
(1)設茶花價格為![]() 元/株,月季價格為y元/株,根據購買
元/株,月季價格為y元/株,根據購買![]() 株茶花與
株茶花與![]() 株月季的費用相同,購買
株月季的費用相同,購買![]() 株茶花與
株茶花與![]() 株月季共需
株月季共需![]() 元列方程組求解可可;
元列方程組求解可可;
(2)設月季有![]() 株,則茶花為(
株,則茶花為(![]() )株,根據“至少需要茶花月季共
)株,根據“至少需要茶花月季共![]() 株,兩種花的總費用不超過
株,兩種花的總費用不超過![]() 元” 列不等式組求解,得出m的范圍,即可確定購置方案;再列出購置總費用關于m的函數解析式,利用一次函數性質結合m的范圍可得其最值情況.
元” 列不等式組求解,得出m的范圍,即可確定購置方案;再列出購置總費用關于m的函數解析式,利用一次函數性質結合m的范圍可得其最值情況.
(1)設茶花價格為![]() 元/株,月季價格為y元/株
元/株,月季價格為y元/株
依題意得![]()
解方程組得![]()
答:茶花價格為20元/株,月季價格為15元/株;
(2)設月季有![]() 株,則茶花為(
株,則茶花為(![]() )株,依據題意得,
)株,依據題意得,
![]()
解得:![]()
設總費用為W,
∴![]() ,
,
∵![]() ,
,
∴W隨![]() 的值的增大而增大,
的值的增大而增大,
∴當![]() 時,
時,![]() 元.
元.


科目:初中數學 來源: 題型:
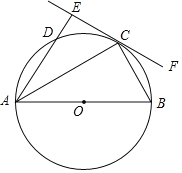
【題目】如圖,AB為⊙O的直徑,C,D為⊙O上的兩點,∠BAC=∠DAC,過點C做直線EF⊥AD,交AD的延長線于點E,連接BC.
(1)求證:EF是⊙O的切線.
(2)若∠CAO=30°,BC=2,求劣弧BC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面的材料:
按照一定順序排列著的一列數稱為數列,數列中的每一個數叫做這個數列的項.排在第一位的數稱為第一項,記為![]() ,排在第二位的數稱為第二項,記為
,排在第二位的數稱為第二項,記為![]() ,依此類推,排在第
,依此類推,排在第![]() 位的數稱為第
位的數稱為第![]() 項,記為
項,記為![]() .所以,數列的一般形式可以寫成:
.所以,數列的一般形式可以寫成:![]() .一般地,如果一個數列從第二項起,每一項與它前一項的差等于同一個常數,那么這個數列叫做等差數列,這個常數叫做等差數列的公差,公差通常用
.一般地,如果一個數列從第二項起,每一項與它前一項的差等于同一個常數,那么這個數列叫做等差數列,這個常數叫做等差數列的公差,公差通常用![]() 表示.如:數列1,3,5,7,…為等差數列,其中
表示.如:數列1,3,5,7,…為等差數列,其中![]() ,公差為
,公差為![]() .
.
根據以上材料,解答下列問題:
(1)等差數列4,7,10,…的公差![]() 為_______,第6項是_______;
為_______,第6項是_______;
(2)如果一個數列![]() 是等差數列,且公差為
是等差數列,且公差為![]() ,那么根據定義可得到:
,那么根據定義可得到:![]() .
.
所以
![]() ;
;
![]() ;
;
![]() ;
;
……
由此,請你填空完成等差數列的通項公:![]() ;
;
(3)![]() 是不是等差數列
是不是等差數列![]() ,
,![]() ,
,![]() ,…的項?如果是,是第幾項?
,…的項?如果是,是第幾項?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小王電子產品專柜以20元/副的價格批發了某新款耳機,在試銷的60天內整理出了銷售數據如下
銷售數據(第x天) | 售價(元) | 日銷售量(副) |
1≤x<35 | x+30 | 100﹣2x |
35≤x≤60 | 70 | 100﹣2x |
(1)若試銷階段每天的利潤為W元,求出W與x的函數關系式;
(2)請問在試銷階段的哪一天銷售利潤W可以達到最大值?最大值為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,長方形ABCD中,AB=8,BC=12,點E是邊BC上一點,BE=5,點F是射線BA上一動點,連接EF,將△BEF沿著EF折疊,使B點的對應點P落在長方形一邊的垂直平分線上,連接BP,則BP的長是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某景區的三個景點![]() 在同一線路上,甲、乙兩名游客從景點
在同一線路上,甲、乙兩名游客從景點![]() 出發,甲步行到景點
出發,甲步行到景點![]() 乙乘景區觀光車先到景點
乙乘景區觀光車先到景點![]() 在
在![]() 處停留一段時間后,再步行到景點
處停留一段時間后,再步行到景點![]() .甲、乙兩人離開景點
.甲、乙兩人離開景點![]() 后的路程
后的路程![]() (米)關于時間
(米)關于時間![]() (分鐘)的函數圖象如圖所示.根據以上信息回答下列問題:
(分鐘)的函數圖象如圖所示.根據以上信息回答下列問題:
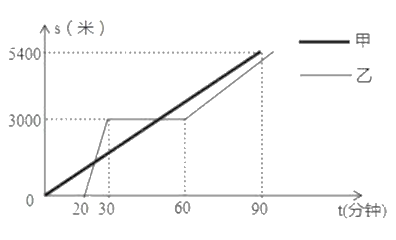
(1)乙出發后多長時間與甲相遇?
(2)若當甲到達景點![]() 時,乙與景點
時,乙與景點![]() 的路程為
的路程為![]() 米,則乙從景點
米,則乙從景點![]() 步行到景點
步行到景點![]() 的速度是多少?
的速度是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 交
交![]() 軸于
軸于![]() ,
,![]() 兩點,交
兩點,交![]() 軸于點
軸于點![]() .直線
.直線![]() 經過點
經過點![]() ,
,![]() .
.
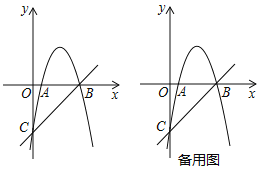
(1)求拋物線的解析式;
(2)過點![]() 的直線交直線
的直線交直線![]() 于點
于點![]() .
.
①當![]() 時,過拋物線上一動點
時,過拋物線上一動點![]() (不與點
(不與點![]() ,
,![]() 重合),作直線
重合),作直線![]() 的平行線交直線
的平行線交直線![]() 于點
于點![]() ,若以點
,若以點![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形是平行四邊形,求點
為頂點的四邊形是平行四邊形,求點![]() 的橫坐標;
的橫坐標;
②連接![]() ,當直線
,當直線![]() 與直線
與直線![]() 的夾角等于
的夾角等于![]() 的
的![]() 倍時,請直接寫出點
倍時,請直接寫出點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
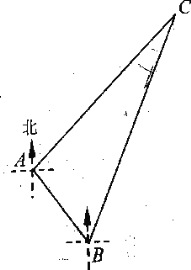
【題目】“雪龍”號考察船在某海域進行科考活動,在點 A 處測得小島C 在它的東北方向上,它沿南偏東37°方向航行 2 海里到達點 B 處,又測得小島C 在它的北偏東23°方向上(如圖所示),求“雪龍”號考察船在點 B 處與小島C 之間的距離.(參考數據: sin22°0.37 , cos22°0.93 , tan 22° 0.40 ,![]() 1.4 ,
1.4 ,![]() 1.7 )
1.7 )
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com