Question

△ABC是等邊三角形，點A與點D的坐標分別是A（4，0），D（10，0）．

（1）如圖1，當點C與點O重合時，求直線BD的解析式；

（2）如圖2，點C從點O沿y軸向下移動，當以點B為圓心，AB為半徑的⊙B與y軸相切（切點為C）時，求點B的坐標；

（3）如圖3，點C從點O沿y軸向下移動，當點C的坐標為C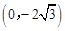時，求∠ODB的正切值．

 

Answer 1

【答案】

解：（1）∵A（4，0），∴OA=4。

∴等邊三角形ABC的高就為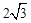。∴B（2，）。

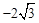設直線BD的解析式為y=kx+b，由題意，得

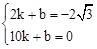，解得：。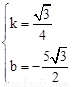

∴直線BD的解析式為：。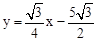

（2）作BE⊥x軸于E，∴∠AEB=90°。

∵以AB為半徑的⊙S與y軸相切于點C，

∴BC⊥y軸。∴∠OCB=90°。

∵△ABC是等邊三角形，∴∠ACB=60°。∴∠ACO=30°。

∴AC=2OA。

∵A（4，0），∴OA=4。∴AC=8。

∴由勾股定理得：OC=。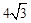

∵BE⊥x軸，∴AE= OA=4。∴OE=8。

∴B（8，）。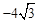

（3）如圖，以點B為圓心，AB為半徑作⊙B，交y軸于點C、E，過點B作BF⊥CE于F，連接AE，

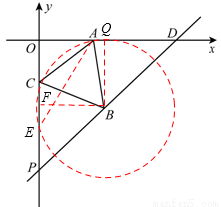
∵△ABC是等邊三角形，

∴AC=BC=AB，∠ABC=∠ACB=∠BAC=60°。

∴∠OEA=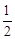∠ABC=30°。∴AE=2OA。

∵A（4，0），∴OA=4。∴AE=8。

在Rt△AOE中，由勾股定理，得OE=。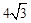

∵C（0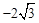，），∴OC=。

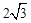在Rt△AOC中，由勾股定理，得AC=。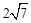

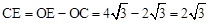∵，BF⊥CE，∴CF=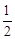CE=。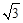

∴。

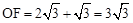在Rt△CFB中，由勾股定理，得，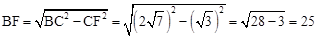

∴B（5，）。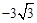

過點B作BQ⊥x軸于點Q，

∴BQ=，OQ=5。∴DQ=5。

∴。

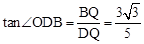【解析】

試題分析：（1）先根據(jù)等邊三角形的性質求出B點的坐標，直接運用待定系數(shù)法就可以求出直線BD的解析式。

（2）作BE⊥x軸于E，就可以得出∠AEB=90°，由圓的切線的性質就可以而出B的縱坐標，由直角三角形的性質就可以求出B點的橫坐標，從而得出結論。

（3）以點B為圓心，AB為半徑作⊙B，交y軸于點C、E，過點B作BF⊥CE于F，連接AE．根據(jù)等邊三角形的性質、圓心角與圓周角之間的關系及勾股定理就可以點B的坐標，作BQ⊥x軸于點Q，根據(jù)正切值的意義就可以求出結論。