
如果拋物線![]() 的頂點在拋物線
的頂點在拋物線![]() 上,同時,拋物線
上,同時,拋物線![]() 的頂點在拋物線
的頂點在拋物線![]() 上,那么,我們稱拋物線
上,那么,我們稱拋物線![]() 與
與![]() 關聯。
關聯。
(1)已知拋物線①![]() ,判斷下列拋物線②
,判斷下列拋物線②![]() ;③
;③![]() 與已知拋物線①是否關聯,并說明理由。
與已知拋物線①是否關聯,并說明理由。
(2)拋物線![]() :
:![]() ,動點P的坐標為(t,2),將拋物線繞點P(t,2)旋轉
,動點P的坐標為(t,2),將拋物線繞點P(t,2)旋轉![]() 得到拋物線
得到拋物線![]() ,若拋物線
,若拋物線![]() 與
與![]() 關聯,求拋物線
關聯,求拋物線![]() 的解析式。
的解析式。
(3)A為拋物線![]() :
:![]() 的頂點,B為與拋物線
的頂點,B為與拋物線![]() 關聯的拋物線頂點,是否存在以AB為斜邊的等腰直角
關聯的拋物線頂點,是否存在以AB為斜邊的等腰直角![]() ,使其直角頂點C在
,使其直角頂點C在![]() 軸上,若存在,求出C點的坐標;若不存在,請說明理由。
軸上,若存在,求出C點的坐標;若不存在,請說明理由。
(1) ∵拋物線①![]() ,其頂點坐標為M(-1,-2).
,其頂點坐標為M(-1,-2).
經驗算,點![]() 在拋物線②上,不在拋物線③上,所以,拋物線①與拋物線③不是關
在拋物線②上,不在拋物線③上,所以,拋物線①與拋物線③不是關![]() 聯的; 拋物線②
聯的; 拋物線②![]() ,其頂點坐標為
,其頂點坐標為![]() (1,2),經驗算點
(1,2),經驗算點![]() 在拋物線①上,所以拋物線①、②是關聯的. (3分)
在拋物線①上,所以拋物線①、②是關聯的. (3分)
(2)拋物線![]() :
:![]() 的頂點
的頂點![]() 的坐標為(-1,-2),因為動點
的坐標為(-1,-2),因為動點![]() 的坐標為
的坐標為
(t,2),所以點![]() 在直線y = 2上,作
在直線y = 2上,作![]() 關于
關于![]() 的對稱點
的對稱點![]() ,分別過點
,分別過點![]() 、
、![]() 作直線y=2的垂線,垂足為
作直線y=2的垂線,垂足為![]() 、
、![]() ,則
,則![]() ,所以點
,所以點![]() 的縱坐標為6. (1分)
的縱坐標為6. (1分)
當![]() 時,
時,![]() ,解之得,
,解之得,![]() ,
,![]() .
.
∴![]() 或
或![]() . (1分)
. (1分)
2.(1)設拋物線![]() 的拋物線為
的拋物線為![]() .
.
因為點![]() 在拋物線
在拋物線![]() 上,∴
上,∴![]() ,
,![]() .
.
∴拋物線![]() 的解析式為
的解析式為![]() (1分)
(1分)
(2)設拋物線![]() 的拋物線為
的拋物線為![]() .
.
因為點![]() 在拋物線
在拋物線![]() 上,∴
上,∴![]() ,
,![]() .
.
∴拋物線![]() 的解析式為
的解析式為![]() ( 1分)
( 1分)


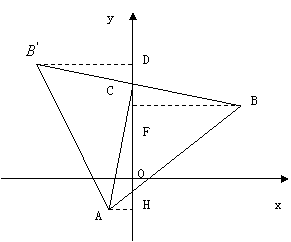

(3)點![]() 為
為![]() 軸上的一動點,以
軸上的一動點,以![]() 為腰作等腰直角△
為腰作等腰直角△![]() ,令
,令![]() 的坐標為
的坐標為![]() ,則點B的坐標
,則點B的坐標![]() 分為兩類:
分為兩類:
①當A,B,C逆時針分布時,如圖中B點,過A、B作y軸的垂線,垂足分別為H、F,則![]() ,∴CF=AH=1,BF=CH=c+2,點B的坐標為(c+2,c-1).
,∴CF=AH=1,BF=CH=c+2,點B的坐標為(c+2,c-1).
當點B在拋物線![]() :
:![]() 上時,
上時,![]() ,解得c=1. (3分)
,解得c=1. (3分)
②當A,B,C順時針分布時,如圖中![]() 點,過
點,過![]() 作y軸的垂線,垂足為D,同理可得點
作y軸的垂線,垂足為D,同理可得點![]() 的坐標為(-c-2,c+1).
的坐標為(-c-2,c+1).
當點![]() 在拋物線
在拋物線![]() :
:![]() 上時,
上時,![]() ,解得
,解得![]() 或
或![]() . (2分)
. (2分)
綜上所述,存在三個符合條件的等腰直角三角形,期中C點的坐標分別為![]() ,
,![]() ,
,![]() . (2分)
. (2分)


科目:初中數學 來源: 題型:
 我們稱拋物線C1與C2關聯.
我們稱拋物線C1與C2關聯.| 1 |
| 8 |
| 1 |
| 8 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 如果拋物線C1的頂點在拋物線C2上,同時,拋物線C2的頂點在拋物線C1上,那么,我們稱拋物線C1與C2關聯.
如果拋物線C1的頂點在拋物線C2上,同時,拋物線C2的頂點在拋物線C1上,那么,我們稱拋物線C1與C2關聯.| 1 | 8 |
查看答案和解析>>
科目:初中數學 來源:2011年湖北省黃岡市黃州區路口中學中考數學模擬試卷(一)(解析版) 題型:解答題
 (x+1)2-2,動點P的坐標為(t,2),將拋物線繞點P(t,2)旋轉180°得到拋物線C2,若拋物線C1與C2關聯,求拋物線C2的解析式.
(x+1)2-2,動點P的坐標為(t,2),將拋物線繞點P(t,2)旋轉180°得到拋物線C2,若拋物線C1與C2關聯,求拋物線C2的解析式. (x+1)2-2的頂點,B為與拋物線C1關聯的拋物線頂點,是否存在以AB為斜邊的等腰直角△ABC,使其直角頂點C在y軸上?若存在,求出C點的坐標;若不存在,請說明理由.
(x+1)2-2的頂點,B為與拋物線C1關聯的拋物線頂點,是否存在以AB為斜邊的等腰直角△ABC,使其直角頂點C在y軸上?若存在,求出C點的坐標;若不存在,請說明理由.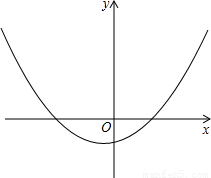
查看答案和解析>>
科目:初中數學 來源:2012年滬科版初中數學九年級上23.4二次函數與一元二次方程練習卷(解析版) 題型:解答題
已知拋物線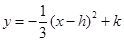 的頂點在拋物線
的頂點在拋物線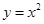 上,且拋物線在
上,且拋物線在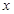 軸上截得的線段長是
軸上截得的線段長是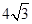 ,求
,求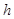 和
和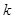 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com