
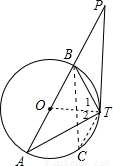
 上是否存在一點C,使得BT2=8TC?若存在,請證明;若不存在,請說明理由.
上是否存在一點C,使得BT2=8TC?若存在,請證明;若不存在,請說明理由.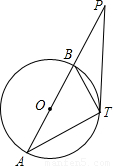
 ,∠P為公共角;故可得△PTB∽△PAT;
,∠P為公共角;故可得△PTB∽△PAT;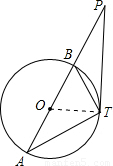 (1)證明:∵∠P=∠P,
(1)證明:∵∠P=∠P, .
.


 新課標快樂提優暑假作業陜西旅游出版社系列答案
新課標快樂提優暑假作業陜西旅游出版社系列答案 暑假銜接培優教材浙江工商大學出版社系列答案
暑假銜接培優教材浙江工商大學出版社系列答案 欣語文化快樂暑假沈陽出版社系列答案
欣語文化快樂暑假沈陽出版社系列答案科目:初中數學 來源: 題型:
 如圖,點在⊙O的直徑AB交TP于P,若PA=18,PT=12,PB=8.
如圖,點在⊙O的直徑AB交TP于P,若PA=18,PT=12,PB=8. | AT |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,點在⊙O的直徑AB交TP于P,若PA=18,PT=12,PB=8.
如圖,點在⊙O的直徑AB交TP于P,若PA=18,PT=12,PB=8. 上是否存在一點C,使得BT2=8TC?若存在,請證明;若不存在,請說明理由.
上是否存在一點C,使得BT2=8TC?若存在,請證明;若不存在,請說明理由.查看答案和解析>>
科目:初中數學 來源:第28章《圓》中考題集(55):28.2 與圓有關的位置關系(解析版) 題型:解答題
 上是否存在一點C,使得BT2=8TC?若存在,請證明;若不存在,請說明理由.
上是否存在一點C,使得BT2=8TC?若存在,請證明;若不存在,請說明理由.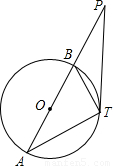
查看答案和解析>>
科目:初中數學 來源:2006年福建省廈門市中考數學試卷(課標A卷)(解析版) 題型:解答題
 上是否存在一點C,使得BT2=8TC?若存在,請證明;若不存在,請說明理由.
上是否存在一點C,使得BT2=8TC?若存在,請證明;若不存在,請說明理由.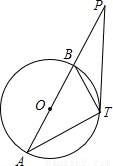
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com