
【題目】如圖,△ABC是⊙O的內接三角形,∠BAD是△ABC的一個外角,∠BAC、∠BAD的平分線分別交⊙O于點E、F.請你在圖上連接EF.(1)證明:EF是⊙O的直徑;(2)請你判斷EF與BC有怎樣的位置關系?并請證明你的結論.

【答案】 (1)詳見解析;(2)EF垂直平分BC,證明詳見解析.
【解析】
(1)先利用角平分線定義和平角定義計算出∠EAF=90°,則利用圓周角定理的推論得到EF為⊙O的直徑;
(2)由AE平分∠BAC得∠BAE=∠CAE,根據圓周角定理得![]() =
=![]() ,于是根據垂徑定理的推論可得EF垂直平分BC.
,于是根據垂徑定理的推論可得EF垂直平分BC.
(1)連接EF.
∵AF平分∠BAD,AE平分∠BAC,∴∠BAF=![]() ∠BAD,∠BAE=
∠BAD,∠BAE=![]() ∠BAC,∴∠BAF+∠BAE=
∠BAC,∴∠BAF+∠BAE=![]() (∠BAD+∠BAC)=
(∠BAD+∠BAC)=![]() ×180°=90°,即∠EAF=90°,∴EF為⊙O的直徑.
×180°=90°,即∠EAF=90°,∴EF為⊙O的直徑.
(2)EF垂直平分BC.理由如下:
∵AE平分∠BAC,∴∠BAE=∠CAE,∴![]() =
=![]() .
.
∵EF為⊙O的直徑,∴EF垂直平分BC.


科目:初中數學 來源: 題型:
【題目】如圖1,△ABC中,AD是∠BAC的角平分線,若AB=AC+CD.那么∠ACB 與∠ABC有怎樣的數量關系? 小明通過觀察分析,形成了如下解題思路:
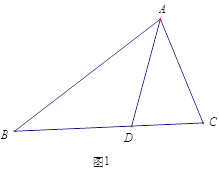
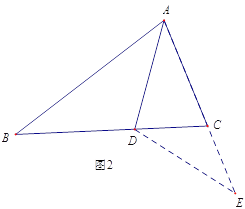
如圖2,延長AC到E,使CE=CD,連接DE,由AB=AC+CD,可得AE=AB,又因為AD是∠BAC的平分線,可得△ABD≌△AED,進一步分析就可以得到∠ACB 與∠ABC的數量關系.
(1) 判定△ABD 與△AED 全等的依據是______________(SSS,SAS,ASA,AAS 從其中選擇一個);
(2)∠ACB 與∠ABC的數量關系為:___________________
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:對稱軸![]() 的拋物線
的拋物線![]() 與
與![]() 軸相交于
軸相交于![]() ,
,![]() 兩點,其中點
兩點,其中點![]() 的坐標為
的坐標為![]() ,且點
,且點![]() 在拋物線
在拋物線![]() 上.
上.

![]() 求拋物線的解析式.
求拋物線的解析式.
![]() 點
點![]() 為拋物線與
為拋物線與![]() 軸的交點.
軸的交點.
①點![]() 在拋物線上,且
在拋物線上,且![]() ,求點
,求點![]() 點坐標.
點坐標.
②設點![]() 是線段
是線段![]() 上的動點,作
上的動點,作![]() 軸交拋物線于點
軸交拋物線于點![]() ,求線段
,求線段![]() 長度的最大值.
長度的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,小華從一個圓形場地的A點出發,沿著與半徑OA夾角為α的方向行走,走到場地邊緣B后,再沿著與半徑OB夾角為α的方向折向行走.按照這種方式,小華第五次走到場地邊緣時處于弧AB上,則α取值范圍是( )

A. 36°![]() 45° B. 45°
45° B. 45°![]() 54° C. 54°
54° C. 54°![]() 72° D. 72°
72° D. 72°![]() 90°
90°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列因式分解的過程,再回答所提出的問題:
![]() .
.
(1)上述分解因式的方法是______________法.
(2)分解![]() 的結果應為___________.
的結果應為___________.
(3)分解因式:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在![]() 中,
中,![]() 于E,
于E,![]() ,D是AE上的一點,且
,D是AE上的一點,且![]() ,連接BD,CD.
,連接BD,CD.

![]() 試判斷BD與AC的位置關系和數量關系,并說明理由;
試判斷BD與AC的位置關系和數量關系,并說明理由;
![]() 如圖2,若將
如圖2,若將![]() 繞點E旋轉一定的角度后,試判斷BD與AC的位置關系和數量關系是否發生變化,并說明理由;
繞點E旋轉一定的角度后,試判斷BD與AC的位置關系和數量關系是否發生變化,并說明理由;
![]() 如圖3,若將
如圖3,若將![]() 中的等腰直角三角形都換成等邊三角形,其他條件不變.
中的等腰直角三角形都換成等邊三角形,其他條件不變.
![]() 試猜想BD與AC的數量關系,請直接寫出結論;
試猜想BD與AC的數量關系,請直接寫出結論;
![]() 你能求出BD與AC的夾角度數嗎?如果能,請直接寫出夾角度數;如果不能,請說明理由.
你能求出BD與AC的夾角度數嗎?如果能,請直接寫出夾角度數;如果不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(問題背景)
如圖1,在四邊形ADBC中,∠ACB=∠ADB=90°,AD=BD,探究線段AC,BC,CD之間的數量關系.
小吳同學探究此問題的思路是:將△BCD繞點D,逆時針旋轉90°到△AED處,點B,C分別落在點A,E處(如圖2),易證點C,A,E在同一條直線上,并且△CDE是等腰直角三角形,所以CE=![]() CD,從而得出結論:AC+BC=
CD,從而得出結論:AC+BC=![]() CD
CD
(簡單應用)
(1)在圖1中,若AC=3, CD=![]() ,則AB= .
,則AB= .
(2)如圖3,AB是⊙O的直徑,點C、D在⊙O上,∠C=45°,若AB=13,BC=12,求CD的長.
(拓展規律)
(3)如圖4,∠ACB=∠ADB=90°,AD=BD,若AC=m,CD=n,則BC的長為 .(用含m,n的代數式表示)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,二次函數
中,二次函數![]() 的圖象與
的圖象與![]() 軸正半軸交于
軸正半軸交于![]() 點.
點.
![]() 求證:該二次函數的圖象與
求證:該二次函數的圖象與![]() 軸必有兩個交點;
軸必有兩個交點;
![]() 設該二次函數的圖象與
設該二次函數的圖象與![]() 軸的兩個交點中右側的交點為點
軸的兩個交點中右側的交點為點![]() ,若
,若![]() ,將直線
,將直線![]() 向下平移
向下平移![]() 個單位得到直線
個單位得到直線![]() ,求直線
,求直線![]() 的解析式;
的解析式;
![]() 在
在![]() 的條件下,設
的條件下,設![]() 為二次函數圖象上的一個動點,當
為二次函數圖象上的一個動點,當![]() 時,點
時,點![]() 關于
關于![]() 軸的對稱點都在直線
軸的對稱點都在直線![]() 的下方,求
的下方,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在第一象限內作射線OC,與x軸的夾角為30°,在射線OC上取點A,過點A作AH⊥x軸于點H.在拋物線y=x2(x>0)上取點P,在y軸上取點Q,使得以P、O、Q為頂點,且以點Q為直角頂點的三角形與△AOH全等,則符合條件的點A的坐標是__________.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com