
【題目】如圖,反比例函數y=![]() 的圖象經過點(﹣1,-2
的圖象經過點(﹣1,-2![]() ),點A是該圖象第一象限分支上的動點,連結AO并延長交另一分支于點B,以AB為斜邊作等腰直角三角形ABC,頂點C在第四象限,AC與x軸交于點D,當
),點A是該圖象第一象限分支上的動點,連結AO并延長交另一分支于點B,以AB為斜邊作等腰直角三角形ABC,頂點C在第四象限,AC與x軸交于點D,當![]() =
=![]() 時,則點C的坐標為 .
時,則點C的坐標為 . 
【答案】![]() (2,-
(2,-![]() )
)
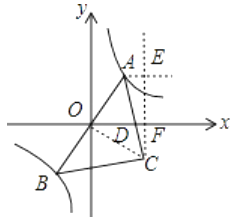
【解析】連接OC,作AE∥x軸、CE∥y軸,交于點E,連接CE交x軸于F點,如圖:
依題可得A、B兩點關于原點O對稱,
∴OA=OB,
∵△ACB是以AB為斜邊的等腰直角三角形,
∴OC=OA=OB,OC⊥AB,
設直線AB解析式為:y=cx(c![]() 0),則直線OC的解析式為:y=-
0),則直線OC的解析式為:y=-![]() x,
x,
∴設A(m,cm)(m> 0),則B(-m,-cm),
∵C在第四象限,
∴C(cm,-m),
又∵AE∥x軸、CE∥y軸,
∴△CAE∽△CDF,
∴![]() =
=![]() ,
,
∵![]() =
=![]() ,AC=AD+CD,
,AC=AD+CD,
∴![]() =
=![]() =
=![]() ,
,
∴E(cm,cm),F(cm,0),
∴![]() =
=![]() =
=![]() ,
,
∴c=![]() ,
,
∴A(m,![]() m)在反比例函數上,
m)在反比例函數上,
又∵(-1,-2![]() )在反比例函數上,
)在反比例函數上,
∴k=(-1)×(-2![]() )=2
)=2![]() ,
,
∴2![]() =
=![]() m2,
m2,
∵m> 0,
∴m=![]() ,
,
∴C(2,-![]() ).
).
【考點精析】本題主要考查了相似三角形的判定與性質的相關知識點,需要掌握相似三角形的一切對應線段(對應高、對應中線、對應角平分線、外接圓半徑、內切圓半徑等)的比等于相似比;相似三角形周長的比等于相似比;相似三角形面積的比等于相似比的平方才能正確解答此題.


科目:初中數學 來源: 題型:
【題目】李師傅加工1個甲種零件和1個乙種零件的時間分別是固定的,現知道李師傅加工3個甲種零件和5個乙種零件共需55分鐘;加工4個甲種零件和9個乙種零件共需85分鐘,求李師傅加工2個甲種零件和4個乙種零件共需多少分鐘.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合與探究
如圖,在平面直角坐標系中,已知拋物線y=ax2+bx﹣8與x軸交于A,B兩點,與y軸交于點C,直線l經過坐標原點O,與拋物線的一個交點為D,與拋物線的對稱軸交于點E,連接CE,已知點A,D的坐標分別為(﹣2,0),(6,﹣8).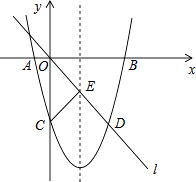
(1)求拋物線的函數表達式,并分別求出點B和點E的坐標;
(2)試探究拋物線上是否存在點F,使△FOE≌△FCE?若存在,請直接寫出點F的坐標;若不存在,請說明理由;
(3)若點P是y軸負半軸上的一個動點,設其坐標為(0,m),直線PB與直線l交于點Q,試探究:當m為何值時,△OPQ是等腰三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】補全下列解題過程:
如圖,OD是∠AOC的平分線,且∠BOC-∠AOB=40°,若∠AOC=120°,求∠BOD的度數.
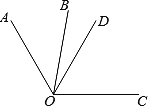
解:∵OD是∠AOC的平分線,∠AOC=120°
∴∠DOC=![]() ∠_______=______°.
∠_______=______°.
∵∠BOC+∠_____=120°,∠BOC-∠AOB=40°
∴∠BOC=80°
∴∠BOD=∠BOC-∠______=______°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,E是AD邊的中點,BE⊥AC,垂足為點F,連接DF,下面四個結論:①CF=2AF;②tan∠CAD=![]() ;
;
③DF=DC;④△AEF∽△CAB;⑤ S四邊形CDEF=![]() S△ABF ,其中正確的結論有( )
S△ABF ,其中正確的結論有( )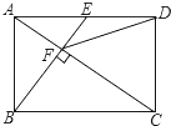
A.2個
B.3個
C.4個
D.5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知兩個等腰直角△ABC和△CDE,它們的兩個直角頂點B、D在直線MN上,過點A、E分別作AG⊥MN,EF⊥MN,垂足分別為G、F.
(1)如圖1,當△ABC和△CDE在△BCD的外部時,請你探索線段EF、DB、AG之間的數量關系,其數量關系為______.
(2)如圖2,將圖1中的△ABC沿BC翻折,其他條件不變,那么(1)中的結論是否仍然成立?若成立,請你給出證明,若不成立,請探索它們的數量關系,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知α是銳角,且點A( ![]() ,a),B(sin30°+cos30°,b),C(﹣m2+2m﹣2,c)都在二次函數y=﹣x2+x+3的圖象上,那么a、b、c的大小關系是( )
,a),B(sin30°+cos30°,b),C(﹣m2+2m﹣2,c)都在二次函數y=﹣x2+x+3的圖象上,那么a、b、c的大小關系是( )
A.a<b<c
B.a<c<b
C.b<c<a
D.c<b<a
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市計劃經銷一些特產,經銷前,圍繞“A:王高虎頭雞,B:羊口咸蟹子,C:桂河芹菜,D:巨淀湖咸鴨蛋”四種特產,在全市范圍內隨機抽取了部分市民進行問卷調查:“我最喜歡的特產是什么?”(必選且只選一種).現將調查結果整理后,繪制成如圖所示的不完整的扇形統計圖和條形統計圖. 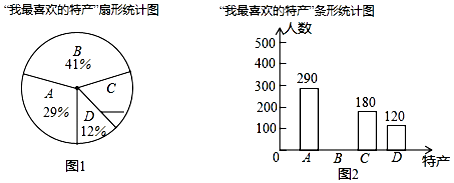
(1)請補全扇形統計圖和條形統計圖;
(2)若全市有110萬市民,估計全市最喜歡“羊口咸蟹子”的市民約有多少萬人?
(3)在一個不透明的口袋中有四個分別寫上四種特產標記A、B、C、D的小球(除標記外完全相同),隨機摸出一個小球然后放回,混合搖勻后,再隨機摸出一個小球,則兩次都摸到A的概率是多少?寫出分析計算過程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】長為5,寬為![]() 的長方形紙片(
的長方形紙片(![]() ),如圖那樣翻折,剪下一個邊長等于長方形寬度的正方形(成為第一次操作);再把剩下的長方形如圖那樣翻折,剪下一個邊長等于此時長方形寬度的正方形(稱為第二次操作);若在第3次操作后,剩下的圖形為正方形,則
),如圖那樣翻折,剪下一個邊長等于長方形寬度的正方形(成為第一次操作);再把剩下的長方形如圖那樣翻折,剪下一個邊長等于此時長方形寬度的正方形(稱為第二次操作);若在第3次操作后,剩下的圖形為正方形,則![]() 的值為__________.
的值為__________.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com