Question

閱讀理解：

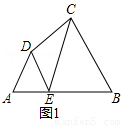
如圖1，在四邊形ABCD的邊AB上任取一點E（點E不與點A、點B重合），分別連接ED，EC，可以把四邊形ABCD分成三個三角形，如果其中有兩個三角形相似，我們就把E叫做四邊形ABCD的邊AB上的相似點；如果這三個三角形都相似，我們就把E叫做四邊形ABCD的邊AB上的強相似點．解決問題：

（1）如圖1，∠A=∠B=∠DEC=55°，試判斷點E是否是四邊形ABCD的邊AB上的相似點，并說明理由；

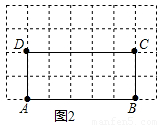
（2）如圖2，在矩形ABCD中，AB=5，BC=2，且A，B，C，D四點均在正方形網格（網格中每個小正方形的邊長為1）的格點（即每個小正方形的頂點）上，試在圖2中畫出矩形ABCD的邊AB上的一個強相似點E；

拓展探究：

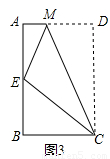
（3）如圖3，將矩形ABCD沿CM折疊，使點D落在AB邊上的點E處．若點E恰好是四邊形ABCM的邊AB上的一個強相似點，試探究AB和BC的數量關系．

 

 

Answer 1

【答案】

解：（1）點E是四邊形ABCD的邊AB上的相似點。理由如下：

∵∠A=55°，∴∠ADE+∠DEA=125°。

∵∠DEC=55°，∴∠BEC+∠DEA=125°。

∴∠ADE=∠BEC。

∵∠A=∠B，∴△ADE∽△BEC。

∴點E是四邊形ABCD的AB邊上的相似點。

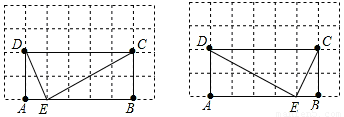
（2）作圖如下：

（3）∵點E是四邊形ABCM的邊AB上的一個強相似點，

∴△AEM∽△BCE∽△ECM。∴∠BCE=∠ECM=∠AEM。

由折疊可知：△ECM≌△DCM，∴∠ECM=∠DCM，CE=CD。

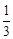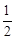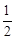∴∠BCE=∠BCD=30°。∴BE=CE=AB。

在Rt△BCE中，，

∴，∴。

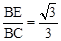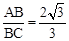【解析】

試題分析：（1）要證明點E是四邊形ABCD的AB邊上的相似點，只要證明有一組三角形相似就行，很容易證明△ADE∽△BEC，所以問題得解。

（2）根據兩個直角三角形相似得到強相似點的兩種情況即可。

（3）因為點E是梯形ABCD的AB邊上的一個強相似點，所以就有相似三角形出現，根據相似三角形的對應線段成比例，可以判斷出AE和BE的數量關系，從而可求出解。