
 如圖,矩形OABC的頂點A、C分別在x軸和y軸上,點B的坐標(biāo)為(2,3),雙曲線y=-$\frac{k}{x}$(x>0)的圖象經(jīng)過的中點D,且與AB交于點E,連接DE
如圖,矩形OABC的頂點A、C分別在x軸和y軸上,點B的坐標(biāo)為(2,3),雙曲線y=-$\frac{k}{x}$(x>0)的圖象經(jīng)過的中點D,且與AB交于點E,連接DE分析 (1)先利用D點為BC的中點得到D(1,3),再利用待定系數(shù)法確定反比例函數(shù)解析式為y=$\frac{3}{x}$,接著利用E點的橫坐標(biāo)為2得到E(2,$\frac{3}{2}$),然后根據(jù)三角形面積公式求解;
(2)根據(jù)相似三角形的性質(zhì),利用相似比可求出CF,然后計算出OF的長,從而得到點F坐標(biāo).
解答 解:(1)∵D點為BC的中點,B(2,3),
∴D(1,3),
把D(1,3)代入y=$\frac{k}{x}$得k=1×3=3,
∴反比例函數(shù)解析式為y=$\frac{3}{x}$,
∵AB⊥x,
∴E點的橫坐標(biāo)為2,
當(dāng)x=2時,y=$\frac{3}{x}$=$\frac{3}{2}$,即E(2,$\frac{3}{2}$),
∴△BDE的面積=$\frac{1}{2}$×(2-1)×(3-$\frac{3}{2}$)=$\frac{3}{4}$;
(2)∵△FBC∽△DEB,
∴$\frac{CF}{BD}$=$\frac{BC}{BE}$,即$\frac{CF}{1}$=$\frac{2}{\frac{3}{2}}$,解得CF=$\frac{4}{3}$,
∴OF=OC-CF=2-$\frac{4}{3}$=$\frac{2}{3}$,
∴點F坐標(biāo)為(0,$\frac{2}{3}$).
點評 本題考查了相似三角形的性質(zhì):相似三角形的對應(yīng)角相等,對應(yīng)邊的比相等;相似三角形(多邊形)的周長的比等于相似比;相似三角形的面積的比等于相似比的平方.也考查了反比例函數(shù)圖象上的點的坐標(biāo)特征.


 字詞句段篇系列答案
字詞句段篇系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 23% | B. | 22% | C. | 19% | D. | 18% |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 5,-3 | B. | 2,-3 | C. | 3,-3 | D. | 2,3 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | m>$\frac{1}{2}$ | B. | m<$\frac{1}{2}$ | C. | m$≥\frac{1}{2}$ | D. | m$≤\frac{1}{2}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
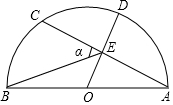 如圖,AB是半圓的直徑,點O為圓心,OA=5,弦AC=8,OD⊥AC,垂足為E,交⊙O于D,連接BE,設(shè)∠BEC=α,則tanα的值為( )
如圖,AB是半圓的直徑,點O為圓心,OA=5,弦AC=8,OD⊥AC,垂足為E,交⊙O于D,連接BE,設(shè)∠BEC=α,則tanα的值為( )| A. | $\frac{3}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{5}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 如圖,MQ為∠NMP的平分線,MP⊥NP,QT⊥MN,垂足分別為P,T,下列結(jié)論不正確的是( )
如圖,MQ為∠NMP的平分線,MP⊥NP,QT⊥MN,垂足分別為P,T,下列結(jié)論不正確的是( )| A. | S△MNQ=$\frac{1}{2}$MN•PQ | B. | ∠MQT=∠MQP | C. | MT=MP | D. | ∠NQP=∠MQT |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | -$\frac{1}{2}$<-2<0.02<0 | B. | -$\frac{1}{2}$<-2<0<0.02 | C. | -2<-$\frac{1}{2}$<0.02<0 | D. | -2<-$\frac{1}{2}$<0<0.02 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com