Question

在Rt△ABC中，AC=3，BC=4．如果以點C為圓心，r為半徑的圓與斜邊AB只有一個公共點，那么半徑r的取值范圍是    ．

Answer 1

【答案】分析：根據直線與圓的位置關系得出相切時有一交點，再結合圖形得出另一種有一個交點的情況，即可得出答案．
解答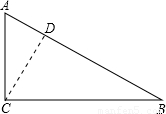：解：過點C作CD⊥AB于點D，
∵AC=3，BC=4．如果以點C為圓心，r為半徑的圓與斜邊AB只有一個公共點，
∴AB=5，
當直線與圓相切時，d=r，圓與斜邊AB只有一個公共點，圓與斜邊AB只有一個公共點，
∴CD×AB=AC×BC，
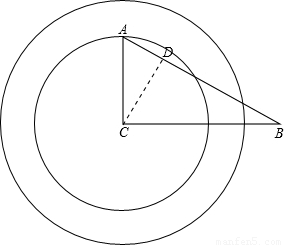
∴CD=r=，
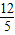
當直線與圓如圖所示也可以有一個交點，
∴3＜r≤4，
故答案為：3＜r≤4或．
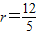
點評：此題主要考查了直線與圓的位置關系，結合題意畫出符合題意的圖形，從而得出答案，此題比較容易漏解．