
【題目】如圖,已知矩形ABCD中,AB=4cm,BC=6cm,動點P從點C開始,以1cm/s的速度在BC的延長線上向右勻速運動,連接AP交CD邊于點E,把射線AP沿直線AD翻折,交CD的延長線于點Q,設點P的運動時間為t.
(1)若DQ=3cm,求t的值;
(2)設DQ=y,求出y與t的函數關系式;
(3)當t為何值時,△CPE與△AEQ的面積相等?
(4)在動點P運動過程中,△APQ的面積是否會發生變化?若變化,求出△APQ的面積S關于t的函數關系式;若不變,說明理由,并求出S的定值.
【答案】
(1)
解:∵四邊形ABCD為矩形,
∴CD=AB=4cm,
∵AP沿直線AD翻折得到AQ,
∴QD=DE=3cm,
∴CE=CD﹣DE=4﹣3=1(cm),
當運動t秒時,則PC=tcm,
∴BP=(t+6)cm,
∵CD∥AB,
∴△PCE∽△PBA,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得t=2
(2)
解:同(1)可知DE=DQ=y,則CE=4﹣y,
同理可得 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
整理可得y= ![]()
(3)
解:不變,理由如下:
由(2)可知當CP=t時,QD= ![]() ,
,
則QE=2QD= ![]() ,CE=4﹣QD=4﹣
,CE=4﹣QD=4﹣ ![]() =
= ![]() ,
,
∴S△AEQ= ![]() QEAD=
QEAD= ![]() ×
× ![]() ×6=
×6= ![]() ,
,
S△CPE= ![]() CPCE=
CPCE= ![]() ×t×
×t× ![]() =
= ![]() ,
,
當S△CPE=S△AEQ時,則有 ![]() =
= ![]() ,
,
解得t=6 ![]() 或t=﹣6
或t=﹣6 ![]() (舍去),
(舍去),
∴當t的值為6 ![]() 秒時,△CPE與△AEQ的面積相等
秒時,△CPE與△AEQ的面積相等
(4)
解:由(3)可知QE= ![]() ,
,
∴S△APQ=S△AQE+S△PQE= ![]() QEAD+
QEAD+ ![]() QECP=
QECP= ![]() QE(AD+CP)=
QE(AD+CP)= ![]() ×
× ![]() ×(t+6)=24,
×(t+6)=24,
∴△APQ的面積為24,不變
【解析】(1)由折疊可知QD=DE,可求得CE,再利用平行可得△PCE∽△PBA,利用相似三角形的性質可得到關于t的方程,可求得t的值;(2)同(1)可用y表示出CE,同理可利用相似三角形的性質可得到關于y與t的函數關系式;(3)利用(2)中的關系式可用t表示出QE、CE,則可用t分別表示出△CPE與△AEQ的面積,由面積相等可得到關于t的方程,可求得t;(4)由(3)可用t分別表示出QE、CE,可表示出△APQ的面積為定值.
【考點精析】認真審題,首先需要了解三角形的面積(三角形的面積=1/2×底×高).


 亮點激活精編提優100分大試卷系列答案
亮點激活精編提優100分大試卷系列答案科目:初中數學 來源: 題型:
【題目】已知等腰三角形的腰長為6cm,底邊長為4cm,以等腰三角形的頂角的頂點為圓心5cm為半徑畫圓,那么該圓與底邊的位置關系是( )
A.相離
B.相切
C.相交
D.不能確定
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某林業部門要考察某種幼樹在一定條件下的移植成活率,在同樣的條件下對這種幼樹進行大量移植,并統計成活情況,記錄如下(其中頻率結果保留小數點后三位)
移植總數(n) | 10 | 50 | 270 | 400 | 750 | 1500 | 3500 | 7000 | 9000 |
成活數(m) | 8 | 47 | 235 | 369 | 662 | 1335 | 3203 | 6335 | 8118 |
成活的頻率 | 0.800 | 0.940 | 0.870 | 0.923 | 0.883 | 0.890 | 0.915 | 0.905 | 0.902 |
由此可以估計幼樹移植成活的概率為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數 ![]() .
.
(1)求證:不論k為任何實數,該函數的圖象與x軸必有兩個交點;
(2)若該二次函數的圖象與x軸的兩個交點在點A(1,0)的兩側,且關于x的一元二次方程k2x2+(2k+3)x+1=0有兩個不相等的實數根,求k的整數值;
(3)在(2)的條件下,關于x的另一方程x2+2(a+k)x+2a﹣k2+6k﹣4=0 有大于0且小于3的實數根,求a的整數值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校為參加高郵市“五運會”廣播操表演,準備從七、八、九三個年級分別選送到位的一男、一女共6名備選人中,每個年級隨機選出1名學生,共3名學生擔任領操員
(1)選出3名領操員中,男生的人數可能是
(2)求選出“兩男一女”3名領操員的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某校綜合實踐活動小組的同學欲測量公園內一棵樹DE的高度,他們在這棵樹正前方一座樓亭前的臺階上A點處測得樹頂端D的仰角為30°,朝著這棵樹的方向走到臺階下的點C處,測得樹頂端D的仰角為60°.已知A點的高度AB為2m,臺階AC的傾斜角∠ACB為30°,且B、C、E三點在同一條直線上.請根據以上條件求出樹DE的高度(測傾器的高度忽略不計).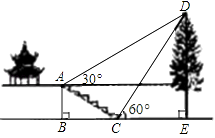
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學活動課上,老師和學生一起去測量學校升旗臺上旗桿AB的高度.如圖,老師測得升旗臺前斜坡FC的坡比為iFC=1:10(即EF:CE=1:10),學生小明站在離升旗臺水平距離為35m(即CE=35m)處的C點,測得旗桿頂端B的仰角為α.已知tanα= ![]() ,升旗臺高AF=1m,小明身高CD=1.6m,請幫小明計算出旗桿AB的高度.
,升旗臺高AF=1m,小明身高CD=1.6m,請幫小明計算出旗桿AB的高度.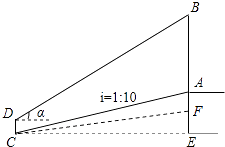
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“元旦”期間,某商場為了吸引顧客購物消費,設計了如圖所示的一個轉盤,轉盤平均分成3份. 
(1)求轉動該轉盤一次所得的顏色是黃色的概率;
(2)請用列表法或畫樹狀圖的方法來說明轉動該轉盤兩次,兩次所得的顏色相同的概率.
(3)該商場設計了如下兩種獎勵方案:方案一,轉動該轉盤一次,若轉得的顏色是黃色則可得獎;方案二,轉動該轉盤兩次,若兩次轉得的顏色相同則可得獎。如果你是顧客,你選擇哪種方案比較劃算?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校園文學社為了解本校學生對本社一種報紙四個版面的喜歡情況,隨機抽查部分學生做了一次問卷調查,要求學生選出自己最喜歡的一個版面,將調查數據進行了整理、繪制成部分統計圖如下:
請根據圖中信息,解答下列問題:
(1)該調查的樣本容量為 , a=%,“第一版”對應扇形的圓心角為°;
(2)請你補全條形統計圖;
(3)若該校有1000名學生,請你估計全校學生中最喜歡“第三版”的人數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com