
【題目】(10分)已知∠MAN=135°,正方形ABCD繞點A旋轉.
(1)當正方形ABCD旋轉到∠MAN的外部(頂點A除外)時,AM,AN分別與正方形ABCD的邊CB,CD的延長線交于點M,N,連接MN.
①如圖1,若BM=DN,則線段MN與BM+DN之間的數量關系是 ;
②如圖2,若BM≠DN,請判斷①中的數量關系是否仍成立?若成立,請給予證明;若不成立,請說明理由;
(2)如圖3,當正方形ABCD旋轉到∠MAN的內部(頂點A除外)時,AM,AN分別與直線BD交于點M,N,探究:以線段BM,MN,DN的長度為三邊長的三角形是何種三角形,并說明理由.

【答案】(1)①MN=BM+DN;②成立;(2)直角三角形.
【解析】試題(1)①如圖1,先證明△ADN≌△ABM,得到AN=AM,∠NAD=∠MAB,得到∠NAD=∠MAB=67.5°.作AE⊥MN于E,由等腰三角形三線合一的性質得出MN=2NE,∠NAE=67.5°.再證明△ADN≌△AEN,得出DN=EN,進而得到MN=BM+DN;
②如圖2,先證明△ABM≌△ADP,得出AM=AP,∠1=∠2=∠3,再計算出∠PAN=135°.然后證明△ANM≌△ANP,得到MN=PN,進而得到MN=BM+DN;
(2)如圖3,將△ABM繞點A逆時針旋轉90°,得到△ADE,連結NE.由旋轉的性質得到DE=BM,AE=AM,∠EAM=90°,∠NDE=90°. 先證明△AMN≌△AEN.得到MN=EN.由DN,DE,NE為直角三角形的三邊,得到以線段BM,MN,DN的長度為三邊長的三角形是直角三角形.
試題解析:(1)①如圖1,若BM=DN,則線段MN與BM+DN之間的數量關系是MN=BM+DN.理由如下:
在△ADN與△ABM中,∵AD=AB,∠ADN=∠ABM,DN=BM,∴△ADN≌△ABM(SAS),∴AN=AM,∠NAD=∠MAB,∵∠MAN=135°,∠BAD=90°,∴∠NAD=∠MAB=![]() (360°﹣135°﹣90°)=67.5°,作AE⊥MN于E,則MN=2NE,∠NAE=
(360°﹣135°﹣90°)=67.5°,作AE⊥MN于E,則MN=2NE,∠NAE=![]() ∠MAN=67.5°.在△ADN與△AEN中,∵∠ADN=∠AEN,∠NAD=∠NAE,AN=AN,∴△ADN≌△AEN(AAS),∴DN=EN,∵BM=DN,MN=2EN,∴MN=BM+DN.故答案為:MN=BM+DN;
∠MAN=67.5°.在△ADN與△AEN中,∵∠ADN=∠AEN,∠NAD=∠NAE,AN=AN,∴△ADN≌△AEN(AAS),∴DN=EN,∵BM=DN,MN=2EN,∴MN=BM+DN.故答案為:MN=BM+DN;
②如圖2,若BM≠DN,①中的數量關系仍成立.理由如下:
延長NC到點P,使DP=BM,連結AP.∵四邊形ABCD是正方形,∴AB=AD,∠ABM=∠ADC=90°.在△ABM與△ADP中,∵AB=AD,∠ABM=∠ADP,BM=DP,∴△ABM≌△ADP(SAS),∴AM=AP,∠1=∠2=∠3,∵∠1+∠4=90°,∴∠3+∠4=90°,∵∠MAN=135°,∴∠PAN=360°﹣∠MAN﹣(∠3+∠4)=360°﹣135°﹣90°=135°.在△ANM與△ANP中,∵AM=AP,∠MAN=∠PAN,AN=AN,∴△ANM≌△ANP(SAS),∴MN=PN,∵PN=DP+DN=BM+DN,∴MN=BM+DN;
(2)以線段BM,MN,DN的長度為三邊長的三角形是直角三角形.理由如下:
如圖3,將△ABM繞點A逆時針旋轉90°,得到△ADE,連結NE.由旋轉的性質得:DE=BM,AE=AM,∠EAM=90°,∠NDE=90°. ∵∠MAN![]() 135°,∴∠EAN
135°,∴∠EAN![]() 360°
360°![]() ∠MAN
∠MAN![]() ∠EAM =135°,∴∠EAN =∠MAN.在△AMN與△AEN中,∵AM=AE,∠MAN=∠EAN,AN=AN,∴△AMN≌△AEN.∴MN=EN.∵DN,DE,NE為直角三角形的三邊,∴以線段BM,MN,DN的長度為三邊長的三角形是直角三角形.
∠EAM =135°,∴∠EAN =∠MAN.在△AMN與△AEN中,∵AM=AE,∠MAN=∠EAN,AN=AN,∴△AMN≌△AEN.∴MN=EN.∵DN,DE,NE為直角三角形的三邊,∴以線段BM,MN,DN的長度為三邊長的三角形是直角三角形.




科目:初中數學 來源: 題型:
【題目】如圖,在正方形網格中,每個小正方形的邊長都為1,點![]() 、點
、點![]() 在網格中的位置如圖所示.
在網格中的位置如圖所示.
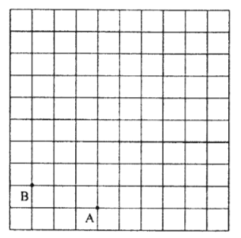
(1)建立適當的平面直角坐標系,使點![]() 、點
、點![]() 的坐標分別為
的坐標分別為![]() 、
、![]() ;
;
(2)點![]() 的坐標為
的坐標為![]() ,在平面直角坐標系中標出點
,在平面直角坐標系中標出點![]() 的位置,連接
的位置,連接![]() 、
、![]() 、
、![]() ,
,
(3)若![]() 各項點的橫坐標不變,縱坐標均乘以
各項點的橫坐標不變,縱坐標均乘以![]() 在圖中做出對應圖形
在圖中做出對應圖形![]() ;
;
(4)![]() 與
與![]() 的位置關系為______;
的位置關系為______;![]() 的面積為______.
的面積為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,設在一個寬度為w的小巷內,一個梯子長為a,梯子的腳位于A點,將梯子的頂端放在一堵墻上Q點時,Q離開地面的高度為k,梯子與地面的夾角為45°:將該梯子的頂端放在另一堵墻上R點時,R點離開地面的高度為h,且此時梯子與地面的夾角為75°,則小巷寬度w=( )
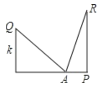
A.hB.kC.aD.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
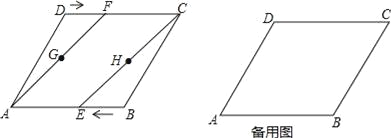
【題目】如圖,在菱形ABCD中,AB=4cm,∠BAD=60°.動點E、F分別從點B、D同時出發,以1cm/s的速度向點A、C運動,連接AF、CE,取AF、CE的中點G、H,連接GE、FH.設運動的時間為ts(0<t<4).
(1)求證:AF∥CE;
(2)當t為何值時,四邊形EHFG為菱形;
(3)試探究:是否存在某個時刻t,使四邊形EHFG為矩形,若存在,求出t的值,若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知正方形ABCD的邊長為6,E,F分別是AB、BC邊上的點,且∠EDF=45°,將△DAE繞點D逆時針旋轉90°,得到△DCM.

(1)求證:EF=MF;
(2)若AE=2,求FC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
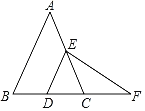
【題目】如圖,在△ABC中,AB=AC,DE∥AB,分別交BC、AC于點D、E,點F在BC的延長線上,且CF=DE.
(1)求證:△CEF是等腰三角形;
(2)連接AD,當AD⊥BC,BC=8,△CEF的周長為16時,求△DEF的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ACD和△BCE中, AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,AD與BE相交于點P,則∠BPD的度數為( )
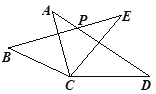
A.110°B.125°C.130°D.155°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com