
如圖,已知直線y=-2x+4與x軸、y軸分別相交于A、C兩點,拋物線y=-2x2+bx+c (a≠0)經過點A、C.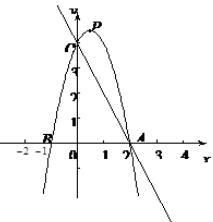
(1)求拋物線的解析式;
(2)設拋物線的頂點為P,在拋物線上存在點Q,使△ABQ的面積等于△APC面積的4倍.求出點Q的坐標;
(3)點M是直線y=-2x+4上的動點,過點M作ME垂直x軸于點E,在y軸(原點除外)上是否存在點F,使△MEF為等腰直角三角形? 若存在,求出點F的坐標及對應的點M的坐標;若不存在,請說明理由.
(1)y=-2x2+2x+4;(2)Q(0,4)或(1,4)或(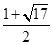 ,-4)或(
,-4)或( ,-4);(3)存在,點F坐標為(0,
,-4);(3)存在,點F坐標為(0, )時,點M的坐標為(
)時,點M的坐標為( ,
, ),點F坐標為(0,-4)時,點M的坐標為(4,-4);點F坐標為(0,1),點M的坐標為(1,2).
),點F坐標為(0,-4)時,點M的坐標為(4,-4);點F坐標為(0,1),點M的坐標為(1,2).
解析試題分析:1)根據直線y=-2x+4求出點A、C的坐標,再利用待定系數法求二次函數解析式解答即可;
(2)根據拋物線解析式求出點P的坐標,過點P作PD⊥y軸于D,根據點P、C的坐標求出PD、CD,然后根據S△APC=S梯形APDO-S△AOC-S△PCD,列式求出△APC的面積,再根據拋物線解析式求出點B的坐標,從而得到AB的長度,然后利用三角形的面積公式求出△ABQ的點Q的縱坐標的值,然后代入拋物線求解即可得到點Q的坐標;
(3)根據點E在x軸上,根據點M在直線y=-2x+4上,設點M的坐標為(a,-2a+4),然后分①∠EMF=90°時,利用點M到坐標軸的距離相等列式求解即可;②∠MFE=90°時,根據等腰直角三角形的性質,點M的橫坐標的長度等于縱坐標長度的一半,然后列式進行計算即可得解.
試題解析:(1)令x=0,則y=4,
令y=0,則-2x+4=0,解得x=2,
所以,點A(2,0),C(0,4),
∵拋物線y=-2x2+bx+c經過點A、C,
∴ ,
,
解得 ,
,
∴拋物線的解析式為:y=-2x2+2x+4;
(2)∵y=-2x2+2x+4=-2(x-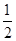 )2+
)2+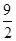 ,
,
∴點P的坐標為(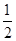 ,
,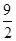 ),
),
如圖,過點P作PD⊥y軸于D,
又∵C(0,4),
∴PD=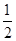 ,CD=
,CD=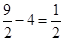 ,
,
∴S△APC=S梯形APDO-S△AOC-S△PCD,
=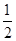 ×(
×(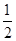 +2)×
+2)×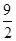 -
-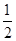 ×2×4-
×2×4-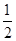 ×
×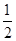 ×
×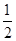
=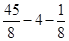
= ,
,
令y=0,則-2x2+2x+4=0,
解得x1=-1,x2=2,
∴點B的坐標為(-1,0),
∴AB=2-(-1)=3,
設△ABQ的邊AB上的高為h,
∵△ABQ的面積等于△APC面積的4倍,
∴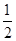 ×3h=4×
×3h=4× ,
,
解得h=4,
∵4<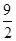 ,
,
∴點Q可以在x軸的上方也可以在x軸的下方,
即點Q的縱坐標為4或-4,
當點Q的縱坐標為4時,-2x2+2x+4=4,
解得x1=0,x2=1,
此時,點Q的坐標為(0,4)或(1,4),
當點Q的縱坐標為-4時,-2x2+2x+4=-4,
解得x1=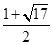 ,x2=
,x2= ,
,
此時點Q的坐標為(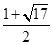 ,-4)或(
,-4)或( ,-4)
,-4)
綜上所述,存在點Q(0,4)或(1,4)或(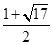 ,-4)或(
,-4)或( ,-4);
,-4);
(3)存在.
理由如下:如圖,
∵點M在直線y=-2x+4上,
∴設點M的坐標為(a,-2a+4),
①∠EMF=90°時,∵△MEF是等腰直角三角形,
∴|a|=|-2a+4|,
即a=-2a+4或a=-(-2a+4),
解得a= 或a=4,
或a=4,
∴點F坐標為(0, )時,點M的坐標為(
)時,點M的坐標為( ,
, ),
),
點F坐標為(0,-4)時,點M的坐標為(4,-4);
②∠MFE=90°時,∵△MEF是等腰直角三角形,
∴|a|=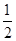 |-2a+4|,
|-2a+4|,
即a=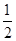 (-2a+4),
(-2a+4),
解得a=1,
-2a+4=2×1=2,
此時,點F坐標為(0,1),點M的坐標為(1,2),
或a= (-2a+4),此時無解,
(-2a+4),此時無解,
綜上所述,點F坐標為(0, )時,點M的坐標為(
)時,點M的坐標為( ,
, ),
),
點F坐標為(0,-4)時,點M的坐標為(4,-4);
點F坐標為(0,1),點M的坐標為(1,2).
考點: 二次函數綜合題.


科目:初中數學 來源: 題型:解答題
在平面直角坐標系 中,拋物線
中,拋物線 與x軸交于點A(-2,0)和點B,與y軸交于點C(0,
與x軸交于點A(-2,0)和點B,與y軸交于點C(0, ),線段AC上有一動點P從點A出發,以每秒1個單位長度的速度向點C移動,線段AB上有另一個動點Q從點B出發,以每秒2個單位長度的速度向點A移動,兩動點同時出發,設運動時間為t秒.
),線段AC上有一動點P從點A出發,以每秒1個單位長度的速度向點C移動,線段AB上有另一個動點Q從點B出發,以每秒2個單位長度的速度向點A移動,兩動點同時出發,設運動時間為t秒.
(1)求該拋物線的解析式;
(2)在整個運動過程中,是否存在某一時刻,使得以A,P,Q為頂點的三角形與△AOC相似?如果存在,請求出對應的t的值;如果不存在,請說明理由.
(3)在y軸上有兩點M(0,m)和N(0,m+1),若要使得AM+MN+NP的和最小,請直接寫出相應的m、t的值以及AM+MN+NP的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,點 是半圓
是半圓 的半徑
的半徑 上的動點,作
上的動點,作 于
于 .點
.點 是半圓上位于
是半圓上位于 左側的點,連結
左側的點,連結 交線段
交線段 于
于 ,且
,且 .
.
(1) 求證: 是⊙O的切線.
是⊙O的切線.
(2) 若⊙O的半徑為 ,
, ,設
,設 .
.
①求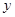 關于
關于 的函數關系式.
的函數關系式.
②當 時,求
時,求 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,拋物線y=-x +4x+5交x軸于A、B(以A左B右)兩點,交y軸于點C.
+4x+5交x軸于A、B(以A左B右)兩點,交y軸于點C.
(1)求直線BC的解析式;
(2)點P為拋物線第一象限函數圖象上一點,設P點的橫坐標為m,△PBC的面積為S,求S與m的函數關系式;
(3)在(2)的條件下,連接AP,拋物線上是否存在這樣的點P,使得線段PA被BC平分,如果不存在,請說明理由;如果存在,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,拋物線 經過點
經過點 ,且與
,且與 軸交于點
軸交于點 、點
、點 ,若
,若 .
.
(1)求此拋物線的解析式;
(2)若拋物線的頂點為 ,點
,點 是線段
是線段 上一動點(不與點
上一動點(不與點 重合),
重合), ,射線
,射線 與線段
與線段 交于點
交于點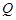 ,當△
,當△ 為等腰三角形時,求點
為等腰三角形時,求點 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,已知直線y=x與拋物線y= x2交于A、B兩點.
x2交于A、B兩點.
(1)求交點A、B的坐標;
(2)記一次函數y=x的函數值為y1,二次函數y= x2的函數值為y2.若y1>y2,求x的取值范圍.
x2的函數值為y2.若y1>y2,求x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
(12分)如圖,在直角坐標系中,已知點A(0,2),點B(-2,0),過點B和線段OA的中點C作直線BC,以線段BC為邊向上作正方形BCDE.
(1)填空:點D的坐標為 ,點E的坐標為 ;
(2)若拋物線y=aa2+ba+c(a≠0)經過A,D,E三點,求該拋物線的解析式;
(3)若正方形和拋物線均以每秒 個單位長度的速度沿射線BC同時向上平移,直至正方形的頂點E落在y軸上時,正方形和拋物線均停止運動.
個單位長度的速度沿射線BC同時向上平移,直至正方形的頂點E落在y軸上時,正方形和拋物線均停止運動.
① 在運動過程中,設正方形落在y軸右側部分的面積為s,求s關于平移時間t(秒)的函數關系式,并寫出相應自變量t的取值范圍;
② 運動停止時,請直接寫出此時的拋物線的頂點坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知二次函數 .
.
(1)在給定的直角坐標系中,畫出這個函數的圖象;
(2)根據圖象,寫出當y<0時,x的取值范圍;
(3)若將此圖象沿x軸向右平移3個單位,請寫出平移后圖象所對應的函數關系式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com