
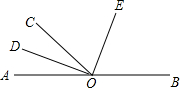
 如圖,點O是AB上的一點,OC為任意一條射線,另有OD,OE分別平分∠AOC,∠BOC.
如圖,點O是AB上的一點,OC為任意一條射線,另有OD,OE分別平分∠AOC,∠BOC. ∠AOC=
∠AOC= ×40°=20°,∠COE=
×40°=20°,∠COE= ∠BOC=70°,
∠BOC=70°, ∠AOC=
∠AOC= ×70°=35°,∠COE=
×70°=35°,∠COE= ∠BOC=55°,
∠BOC=55°, ∠AOC,∠COE=
∠AOC,∠COE= ∠BOC,
∠BOC, ∠AOC+
∠AOC+ ∠BOC=
∠BOC= (∠AOC+∠BOC)=
(∠AOC+∠BOC)= ∠AOB=90°.
∠AOB=90°. ∠AOC=20°,∠COE=
∠AOC=20°,∠COE= ∠BOC=70°,然后利用∠DOE=∠COD+∠COE進行計算;
∠BOC=70°,然后利用∠DOE=∠COD+∠COE進行計算; ∠AOC=35°,∠COE=
∠AOC=35°,∠COE= ∠BOC=55°,然后利用∠DOE=∠COD+∠COE進行計算;
∠BOC=55°,然后利用∠DOE=∠COD+∠COE進行計算; ∠AOC,∠COE=
∠AOC,∠COE= ∠BOC,則∠DOE=∠COD+∠COE=
∠BOC,則∠DOE=∠COD+∠COE= ∠AOC+
∠AOC+ ∠BOC=
∠BOC= (∠AOC+∠BOC)=
(∠AOC+∠BOC)= ∠AOB=90°.
∠AOB=90°.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
 23、已知,如圖,點C是AB上一點,分別以AC,BC為邊,在AB的同側作等邊三角形△ACD和△BCE.
23、已知,如圖,點C是AB上一點,分別以AC,BC為邊,在AB的同側作等邊三角形△ACD和△BCE.查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,點O是AB上的一點,OC為任意一條射線,另有OD,OE分別平分∠AOC,∠BOC.
如圖,點O是AB上的一點,OC為任意一條射線,另有OD,OE分別平分∠AOC,∠BOC.查看答案和解析>>
科目:初中數學 來源:同步題 題型:單選題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com